CAT Quant: Mensuration – Important Formulas and Concepts
Basics
- Mensuration is the branch of geometry that deals with the measurement of length, area and volume. Key terms used in mensuration are briefly explained below :-
- Length: The measurement of the longest side of a geometric figure.
- Area: The measure of the space enclosed by a geometric figure.
- Volume: The measure of the space occupied by a three-dimensional figure.
- Surface Area: The total area of the surface of a three-dimensional figure.
- Perimeter: The total distance around the boundary of a two-dimensional figure.
Area of Plane Figures
- The area of a plane figure refers to the measure of the space enclosed by the boundaries of the figure in a two-dimensional plane. It represents the amount of surface or space covered by the figure. The formulae for areas of various plane figures are discussed below.
Triangles
- The area of a triangle is represented by the symbol A. For any triangle, the lengths of the three sides are represented by a, b and c and the angles opposite these sides are represented by A, B and C respectively.
- For any triangle in general –
- when the lengths of three sides a, b, c are given, \( \\ \) \(Area = \sqrt{s(s-a)(s-b)(s-c)} \\ \) where, \( s=\frac{a+b+c}{2}=\frac{p}{2} \) (This is called Heron’s formula.)
- when base (b) and altitude (height) to that base are given, \( \\ Area = \frac{1}{2} (base)(altitude)=\frac{1}{2}bh \)
- \( Area = \frac{1}{2}ab(sinC) = \frac{1}{2} bc(sinA) = \frac{1}{2} ca(sinB) \)
- \( Area = \frac{abc}{4R} \) where, R is the circumradius of the triangle.
- \( Area = rs \) where, r is the inradius of the triangle and s the semi-perimeter. \( \\ \) Also, \( r = s-h \)
- For a right angled triangle –
- \( Area =\frac{1}{2}(Product \ of \ the \ sides \ containing \ the \ right \ angle) \\ \hspace{1cm} = \frac{1}{2}(base)(perpendicular) \)
- For an equilateral triangle –
- \( Area = \frac{\sqrt{3}a^{2}}{4} \) where, “a” is the side of the triangle \( \\ \) The height of an equilateral triangle \( =\frac{\sqrt{3}a}{2} \)
- For an isosceles triangle –
- \( Area = \frac{b}{4}\sqrt{4a^{2}-b^{2}} \) where, “a” is length of each of the two equal sides and b is the third side.
Quadrilaterals
- For any quadrilateral –
- \( Area \ of \ the \ quadrilateral = \frac{1}{2}(One \ diagonal) (Sum \ of \ the \ offsets \ drawn \ to \ that \ diagonal) \\ \) For the given figure, Area of quadrilateral (ABCD) \( = \frac{1}{2} (AC)(BE + DF) \\ \)
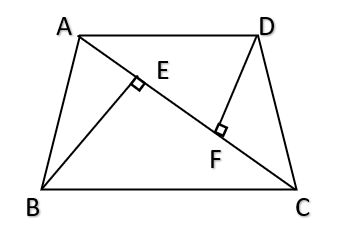
- \( Area \ of \ the \ quadrilateral = \frac{1}{2}(One \ diagonal) (Sum \ of \ the \ offsets \ drawn \ to \ that \ diagonal) \\ \) For the given figure, Area of quadrilateral (ABCD) \( = \frac{1}{2} (AC)(BE + DF) \\ \)
- For a cyclic quadrilateral – in which the lengths of the four sides are a, b, c and d
- \( Area=\sqrt{(s-a)(s-b)(s-c)(s-d)} \\ \) where s is the semi-perimeter, i.e., \( s=\frac{(a+b+c+d)}{2} \)
- For a trapezium –
- \( Area \ of \ a \ trapezium = \frac{1}{2}(Sum \ of \ parallel \ sides) (Distance \ between \ them) \\ \) For the given figure, \( Area = \frac{1}{2}(AD+BC)(AF) \\ \)
- \( Area \ of \ a \ trapezium = \frac{1}{2}(Sum \ of \ parallel \ sides) (Distance \ between \ them) \\ \) For the given figure, \( Area = \frac{1}{2}(AD+BC)(AF) \\ \)
- For a parallelogram –
- \( Area = (Base) \times (Height) \)
- \( Area = Product \ of \ two \ adjacent \ sides \ (Sine of included angle) \) \( \\ \)
- For a rhombus –
- \( Area =\frac{1}{2} (Product \ of \ the \ diagonals) \\ \hspace{1cm} = \frac{1}{2}(d_{1} \times d_{2}) \)
- \( Perimeter = 4(Side \ of \ the \ rhombus) \) \( \\ \)
- For a rectangle –
- \( Area = (Length)(Breadth) = lb \)
- \( Perimeter = 2(l+b) \) , where l and b are the length and the breadth of the rectangle respectively \)
- \( Diagonal (d) = \sqrt{l^2+b^2} \) \( \\ \)

- For a square –
- \( Area = (Side)^2 \)
- \( Area = \frac{1}{2} (Diagonal)^2 \)
- \( Perimeter = 4(Side) \)
- \( Diagonal = \sqrt{2} (side) \) \( \\ \)
- For a polygon –
- \( Area \ of \ a \ regular \ polygon = \frac{1}{2}(Perimeter)(Perpendicular \ distance \ from \ the \ center \ of \ the \ polygon \ to \ any \ side) \\ \) (Note that the center of a regular polygon is equidistant from all its sides).
- For a polygon which is not regular, the area has to be found out by dividing the polygon into suitable number of quadrilaterals and triangles and adding up the areas of all such figures present in the polygon.
Circle
- \( Area \ of \ the \ circle = ar² \) where, r is the radius of the circle.
- \( Circumference = 2 \pi г \)
- \( Sector \ of \ a \ circle \ = Length \ of \ arc = \frac{\theta}{360°}(2πг) \\ Area = \frac{\theta}{360°}(πr^2) \) where \( \theta \) is the angle of the sector in degrees and r is the radius of the circle.
- \(Area = (1/2)Ir \) where, l is length of arc and r is radius.
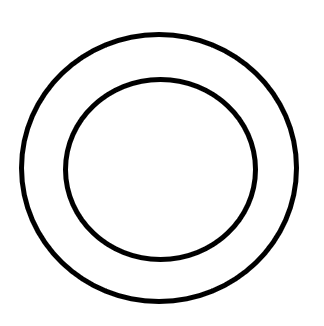
- Ring – Ring is the space enclosed by two concentric circles. \( \\ Area = \pi R^2 – \pi r² = \pi (R+r)(R-r) \) where, R is the radius of the outer circle and r is the radius of the inner circle. \( \\ \)
Area and Volume of Solids
- Solids are three-dimensional objects which, in addition to area, have volume also. For solids, two different types of areas are defined
- Lateral surface area or curved surface area – lateral surface area is the area of the lateral surfaces of the solid.
- Total surface area – Total surface area includes the areas of the top and the bottom surfaces also of the solid. Hence, Total surface area = Lateral surface area + Area of the top face + Area of the bottom face.
- Euler’s Rule – For any solid, whose faces are regular polygons, there is a definite relationship between the number of vertices, the number of sides and the number of edges of the solid. This relationship is given by “Euler’s Rule”. $$ \\ Number \ of \ faces + Number \ of \ vertices = Number \ of \ edges + 2 $$ .
Prism
- A right prism is a solid whose top and bottom faces (bottom face is called base) are parallel to each other and are identical polygons (of any number of sides) that are parallel.
- The faces joining the top and bottom faces are rectangles and are called lateral faces.
- There are as many lateral faces as there are sides in the base.
- In a right prism, if a perpendicular is drawn from the center of the top face, it passes through the center of the base.
- For any prism –
- \( Lateral \ Surface \ Area = Perimeter \ of \ base \ (Height \ of \ the \ prism) \)
- \( Total \ Surface \ Area = Lateral \ Surface \ Area + 2 x (Area \ of \ base) \)
- \( Volume = (Area \ of \ base) \times (Height \ of \ the \ prism ) \) \( \\ \)
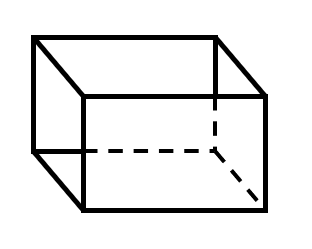
Cuboid
- A right prism whose base is a rectangle is called a cuboid or rectangular solid.
- If a and b are respectively the length and breadth of the base and h, the height of the prism, then –
- \( Volume = lbh \)
- \( Lateral \ Surface \ Area = 2(l+ b)h \)
- \( Total \ Surface \ Area = 2(l + b)h + 2lb\) \( \ = 2(lb + lh + bh) \)
- \( Longest \ diagonal \ of \ the \ cuboid = \sqrt{l² + b² +h²} \) \( \\ \)
Cube
- A right prism whose base is a square and height is equal to the side of the base is called a cube.
- If a is the edge of the cube, then –
- \( Volume = a³\)
- \( Lateral \ Surface \ Area = 4a^2 \)
- \( Total \ Surface \ Area = 6a^2 \)
- \( Diagonal \ of \ the \ cube = a \sqrt{3} \) \( \\ \)
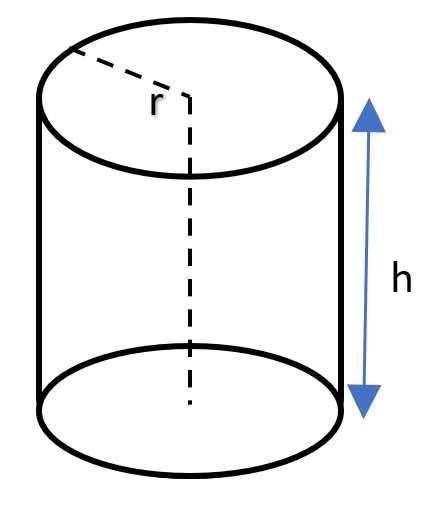
Cylinder
- A cylinder is equivalent to a right prism whose base is a circle.
- A cylinder has a single curved surface as its lateral faces.
- If r is the radius of the base and h is the height of the cylinder, then –
- \( Volume = r²h \)
- \( Curved \ Surface \ Area = 2\pi rh \)
- \( Total \ Surface \ Area = 2 \pi rh+ 2 \pi r² \) \( \ = 2 \pi r(h + r) \) \( \\ \)
- A hollow cylinder has a cross-section of a ring.
- Volume of the material contained in a hollow cylindrical shell \( = \pi (R^2 – r^2)h \) where, R is the outer radius, r is the inner radius and h the height.
Pyramid
- A solid whose base is a polygon and whose faces are triangles is called a pyramid.
- The triangular faces meet at a common point called vertex. The perpendicular from the vertex to the base is called the height of the pyramid.
- A pyramid whose base is a regular polygon and the foot of the perpendicular from the vertex to the base coincides with the center of the base, is called a right pyramid.
- The length of the perpendicular from the vertex to any side of the base (note that this side will be the base of one of the triangular lateral faces of the prism) is called the slant height of the prism.
- \( Volume = \frac{1}{3}(Area \ of \ base) (Height) \)
- \( Lateral \ Surface \ Area = \frac{1}{2}(Perimeter \ of \ the \ base) (Slant \ height) \)
- \( Total \ Surface \ Area = (Lateral \ Surface \ Area) + (Area \ of \ the \ base) \) \( \\ \)
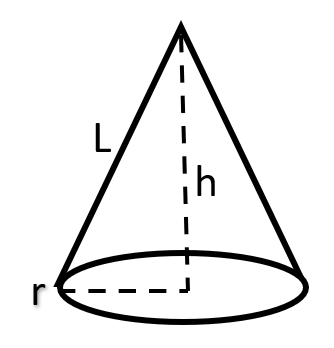
Cone
- A cone is equivalent to a right pyramid whose base is a circle.
- The lateral surface of a cone does not consist of triangles like in a right pyramid but is a single curved surface.
- If r is the radius of the base of the cone, h is height of the cone and I is the slant height of the cone, then –
- \( l^{2} = r^{2}+h^{2} \)
- \( Volume = \frac{1}{3} \pi r^{2}h \)
- \( Curved \ Surface \ Area = \pi rl \)
- \( Total \ Surface \ Area = \pi rl+\pi r^2 \) \( \ = \pi r (l+r) \) \( \\ \)
- A cone can be formed by folding a sector of a circle and joining together its straight edges. If the radius of the sector is R and the angle of the sector is “\( \theta \) “, then we have the following relationships between the length of the arc and area of the sector on one hand and base perimeter of the cone and curved surface area of the cone on the other hand.
- Radius of the sector = Slant height of the cone \( \\ \longrightarrow R = l \)
- Length of the arc of the sector = Circumference of the base of the cone \( \\ \longrightarrow \frac{\theta}{360}(2\pi R)=2\pi r \Rightarrow r = \frac{\theta R}{360} \)
- Area of the sector = Curved surface area \( \\ \longrightarrow \frac{\theta}{360}\pi R^{2}=\pi rl \)
Cone Frustum
- If a cone is cut into two parts by a plane parallel to the base, the portion that contains the base is called the frustum of a cone.
- If r is the top radius, R the radius of the base, h the height and l the slant height of a frustum of a cone then –
- \( l^{2}=(R-r)^{2}+h^{2} \)
- \( Volume = \frac{1}{3} \pi h (R² + Rr + r²) \)
- \( Lateral \ Surface \ Area = \pi l(R+r) \)
- \( Total \ Surface \ Area =\pi (R^{2}+r^{2}+Rl+rl) \) \( \\ \)
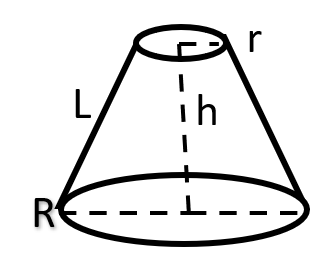
- If H is the height of the complete cone from which the frustum is cut, then from similar triangles, we can write the following relationship –
- \( \frac{r}{R}=\frac{H-h}{H} \)
Frustum of a Pyramid
- The part of a pyramid left after cutting of a portion at the top by a plane parallel to the base is called a frustum of a pyramid.
- If A1 is the area of the base, A2 the area of the top and h the height of the frustum, then –
- \( Volume =\frac{1}{3}h(A_{1}+A_{2}+\sqrt{A_{1}A_{2}}) \)
- \( Lateral \ Surface \ Area = \frac{1}{2}(Sum \ of \ perimeters \ of \ base \ and \ top) \times (Slant height) \)
- \( Total \ Surface \ Area = (Lateral \ Surface \ Area) +A_{1}+A_{2} \) \( \\ \)
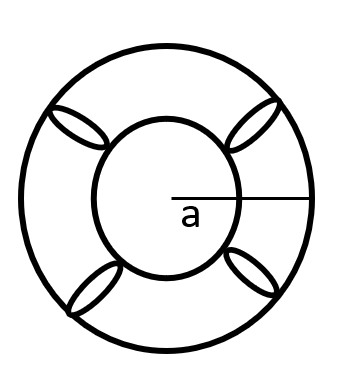
Torus
- A torus is a three-dimensional figure produced by the revolution of a circle about an axis lying in its plane but not intersecting the circle.
- The shape of the rubber tube in a bicycle (when it is inflated fully) is an example of a torus.
- A torus is also referred to as a solid ring.
- If r is the radius of the circle that rotates and a is the distance between the center of the circle and the axis of revolution, then –
- \( Volume = 2 \pi ^{2} r^{2} a \)
- \( Surface \ Area = 4 \pi ^{2} ra \) \( \\ \)
Sphere
- A sphere is a three-dimensional geometric object that is perfectly round in shape.
- It is defined as the set of all points in space that are equidistant from a given point called the center.
- If r is the radius of the sphere, then –
- \( Volume = \frac{4}{3} \pi г^3 \)
- \( Surface \ Area = 4 \pi r^2 \)
- The of a hemisphere is equal to half the surface area of a sphere, i.e.,
Hemisphere
- A hemisphere is a three-dimensional geometric shape that is half of a sphere.
- It is formed by cutting a sphere along a plane passing through its center. This results in two equal parts, each resembling half of a sphere.
- If r is the radius of a hemisphere, then –
- \( Volume = \frac{2}{3} \pi г^3 \)
- \( Curved \ Surface \ Area= 2\pi r^{2} \)
Note: Often we use symbols in two different ways. In some problems we use symbols to represent quantities (like length, area, volume). In other problems we use symbols to represent only a number.
Read concepts and formulas for: Number Systems
Read more about AI practice Platform here: https://www.learntheta.com/cat-quant/