CAT Quant Number Systems – Important Formulas and Concepts
Real Numbers
Real numbers are a fundamental concept in mathematics and represent a wide range of quantities, including integers, fractions, decimals, and irrational numbers.
The set of real numbers, denoted by the symbol “R”, includes all numbers that can be represented on the number line.
Classification of Real Numbers
Rational Numbers
A number which can be expressed in the form p/q where p and q are integers and q\( \ne \) 0 is called a rational number. For example : 6, -31, 73/2, -7/23 etc.
Between any two numbers, there can be infinite number of other rational numbers.
Real numbers an be further be classified into two categories –
Terminating Decimals –
A terminating decimal is a decimal number that ends or terminates after a finite number of digits.
In other words, the decimal representation of a terminating decimal stops at some point.
For example, the fraction 1/4 is equal to 0.25 in decimal form.
Non-Terminating decimals –
A non-terminating decimal is a decimal number that does not end or terminate but continues indefinitely without repeating a pattern.
These decimals do not end but repeat a pattern of digits indefinitely.
For example, the fraction 1/3 has a decimal representation of 0.333…, where the digit 3 repeats infinitely.
Non-repeating non-terminating decimals :
These decimals do not end and do not repeat any pattern of digits (such numbers are referred to as irrational numbers).
An example is the decimal representation of the irrational number π (pi): 3.141592653589793…
Irrational Number
Numbers which are not rational but which can be represented by points on the number line are called irrational numbers.
Examples for irrational numbers are \( \pi , \mathrm{e} , \sqrt{2} , \sqrt{7} , \sqrt[4]{5} \) etc.
Between any two numbers, there are infinite number of irrational numbers.
Any non-terminating non-recurring decimal is an irrational number.
Integers
Integers are whole numbers, including both positive and negative numbers, as well as zero.
All integers are rational numbers. The set of integers is denoted by the symbol “Z”.
They do not have any fractional or decimal parts.
Integers include –
Positive Integers: These are whole numbers greater than zero. Examples include 1, 2, 3, 4, and so on.
Negative Integers: These are whole numbers less than zero. Examples include -1, -2, -3, -4, and so on.
Zero: Zero is considered an integer but is neither positive nor negative.
Positive Integers can be classified as Prime Numbers and Composite Numbers.
Prime Numbers –
A number other than 1 which does not have any factor apart from one and itself is called a prime number.
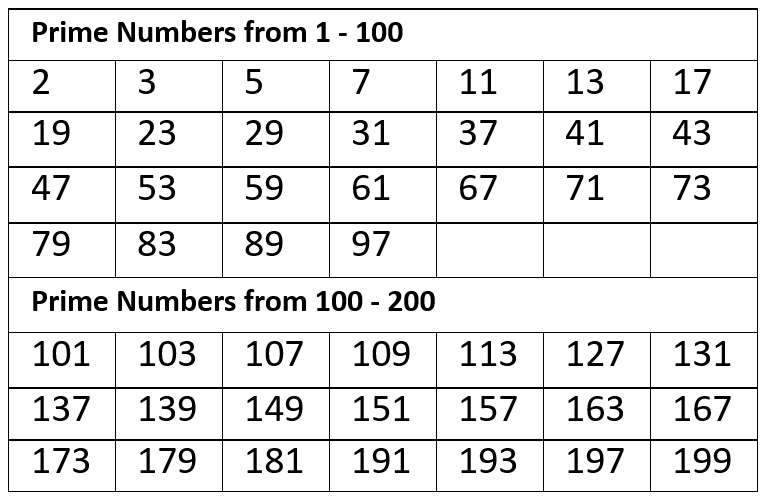
Examples for prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, etc.
Every prime number greater than 3 can be written in the form of (6k+1) or (6k 1) where k is an integer. \( \\ \)
Composite Numbers –
Any natural number which has more than two factors is a composite number. In other words, a composite number is a number which has factors besides one and itself.
Examples for composite numbers are 4, 6, 8, 9, 10, 14, 15, etc.
NOTE: The number 1 is neither prime nor composite. The only prime number that is even is 2.
There are 15 prime numbers between 1 and 50 and 10 prime numbers between 50 and 100. So, there are a total of 25 prime numbers between 1 and 100.
Even and Odd numbers–
Numbers divisible by 2 are called even numbers whereas numbers that are not divisible by 2 are called odd numbers.
Examples for even numbers are 2, 4, 6, 8, 10, etc. Examples for odd numbers are 1, 3, 5, 7, 9, etc.
Important Points relating to Even and Odd Numbers –
Every even number ends in 0, 2, 4, 6 or 8.
The sum of any number of even numbers is always even.
The sum of odd number of odd numbers (i.e., the sum of 3 odd numbers, the sum of 5 odd numbers, etc.) is always odd.
The sum of even number of odd numbers (i.e., the sum of 2 odd numbers, the sum of 4 odd numbers, etc.) is always even.
The product of any number of odd numbers is always odd.
The product of any number of numbers where there is at least one even number is even.
Perfect Numbers –
A number is said to be a perfect number if the sum of all its factors excluding itself (but including 1) is equal to the number itself.
For example, 6 is a perfect number because the factors of 6, l.e., 1, 2 and 3 add up to the number 6 itself.
Other examples of perfect numbers are 28, 496, 8128, etc.
Hierarchy of Arithmetic Operations
The hierarchy of arithmetic operations are given by a rule called BODMAS rule.
The operations have to be carried out in the order in which they appear in the word BODMAS, where different letters of the word BODMAS stand for the following operations:
B – Brackets
O – Of
D – Division
M – Multiplication
A – Addition
S – Subtraction
There are four types of brackets:
Vinculum: This is represented by a bar on the top of the numbers. For example, \( 2+3- \overline{4+3} \); Here, the figures under the vinculum have to be calculated as 4 + 3 first and the “minus” sign before 4 is applicable to 7. Thus the given expression is equal to 2+ 3-7 which is equal to -2.
Simple Brackets: These are represented by ()
Curly Brackets: These are represented by {}
Square Brackets: These are represented by []
The brackets in an expression have to be opened in the order of vinculum, simple brackets, curly brackets and square brackets, i.e., [{() } ] to be opened from inside outwards.
Two operations that have not been mentioned in the BODMAS rule are taking powers and extracting roots, viz, involution and evolution respectively. When these operations are also involved in expressions, there is never any doubt about the order in which the steps of the simplification should be taken. The sign for root extraction is a variant of the vinculum and for powers, brackets are used to resolve ambiguities in the order.
Properties of Division
A number when divided by “d” leaving a remainder of “r” is of the form (dq+r) where “q” is some integer from 0, 1, 2, ……….
When a number “N” is divided by divisor “d” if the remainder is “r”, then the number (N-r) is exactly divisible by “d” or in other words, when (N-r) is divided by “d” the remainder is 0.
When a number N is divided by a divisor “d”, if the remainder is “r”, then
the largest multiple of “d” which is less than or equal to N, is obtained by subtracting from N, i.e., (N-r) will be the largest multiple of “d” which is less than or equal to N.
For example, when 27 is divided by 5, the remainder is 2; so (27-2), i.e., 25 is the largest multiple of 5 less than 27.
the smallest multiple of “d” which is greater than or equal to N is obtained by adding (d-r) to N, i.e., N+(d-r) will be the smallest multiple of “d” which is greater than N.
For example, when 49 is divided by 8, the remainder is 1; hence the smallest multiple of 8 which is greater than 48 s~49+(8-1)=56
When a division is split into a sum of two divisions (with the same divisor as the original divisor), the original remainder will be equal to the sum of the remainders of the two individual divisions. Similarly, when a division is split into difference of two divisions, the original remainder will be equal to the difference of the remainders of the two divisions.
For example, if we take the division 15/6 (where the remainder is 3), and write it as a SUM of two divisions 8/6 and 7/6 (where the remainders are respectively 2and 1), the original remainder is equal to the sum of the two remainders 2 and 1. \( \\ \frac{15}{6}=\frac{8}{6}+\frac{7}{6} \) Remainder \( 3 = 2+1 \)
In a division, if the dividend (the number which is being divided) is multiplied by a certain factor and then divided by the same divisor, then the new remainder will be obtained by multiplying the original remainder by the same factor with which the dividend has been multiplied.
For example, when 11 is divided by 8, the remainder is 3. When the dividend 11 is multiplied by 2, we get 22 and when this number is divided by 8, the remainder is 6 which is same as the original remainder 3 multiplied by 2.
Factors, Multiples and Co-primes
Factors –
If one number divides a second number exactly, then the first number is said to be a factor of the second number. Factors are also called sub-multiples or divisors.
For example, 6 is a factor of 12; 3 is a factor of 21.
Multiples –
If one number is divisible exactly by a second number, then the first number is said to be a multiple of the second number.
For example, 12 is a multiple of 6; 24 is a multiple of 3.
Co-Primes –
Two numbers are said to be relative primes or co-primes if they do not have any common factor other than 1.
For example, the numbers 17 and 16 do not have any common factors and hence they are relative primes.
None of the two numbers may individually be prime and still they can be relative primes.
Unity is a relative prime to all numbers.
Rules for divisibility
Divisibility by 2 –
A number divisible by 2 will have an even number as its last digit.
For example : 732, 98746, 78, etc.
Divisibility by 3 –
A number is divisible by 3 if the sum of its digits is a multiple of 3.
For example, take the number 213, the sum of the digits is 2+1+3 = 6 which is a multiple of 3. Hence, the given number 213 is divisible by 3.
Divisibility by 4 –
A number is divisible by 4 if the number formed with its last two digits is divisible by 4.
For example, if we take the number 8536, the last two digits form 36. Since this number 36 is divisible by 4. the number 8536 is divisible by 4.
Divisibility by 5 –
A number is divisible by 5 if its last digit is 5 or zero.
For example: 1525, 90, 7650, etc.
Divisibility by 6 –
A number is divisible by 6 if it is divisible both by 2 and 3.
For example: 18, 42, 96, etc.
Divisibility by 7 –
If the difference between the number of tens in the number and twice the units digit is divisible by 7, then the given number is divisible by 7. Otherwise, it is not divisible by 7.
Take the units digit of the number, double it and subtract this figure from the remaining part of the number. If the result so obtained is divisible by 7, then the original number is divisible by 7. If that result is not divisible by 7, then the number is not divisible by 7.
For example, let us take the number 595. The units digit is 5 and when it is doubled, we get 10. The remaining part of the number is 59. If 10 (which is the units digit doubled) is subtracted from 59 we get 49. Since this result 49 is divisible by 7, the original number 595 is also divisible by 7.
Divisibility by 8 –
A number is divisible by 8, if the number formed by the last 3 digits of the number is divisible by 8.
For example, the number 3816 is divisible by 8 because the last three digits form the number 816, which is divisible by 8. Similarly, the numbers 14328, 18864 etc. are divisible by 8. If we take the number 48764, it is not divisible by 8 because the last three digits number 764 Is not divisible by 8.
Note –
In general, if the number formed by the last n digits of a number is divisible by 2n, the number is divisible by 2n.
Divisibility by 9 –
A number is divisible by 9 if the sum of its digits is a multiple of 9.
For example, if we take the number 792, the sum of the digits of this number is 7+9+2 which is 18. Since this sum 18 is a multiple of 9, the number 792 is divisible by 9.
Divisibility by 10 –
A number divisible by 10 should end in zero.
For example: 680, 72820, 5790, etc.
Divisibility by 11 –
A number is divisible by 11 if the sum of the alternate digits is the same or they differ by multiples of 11 – that is, the difference between the sum of digits in odd places in the number and the sum of the digits in the even places in the number should be equal to zero or a multiple of 11.
For example, if we take the number 785345, the sum of the digits in odd places is 16 and the sum of the digits in even places is also 16. Since these two sums are equal, the given number is divisible by 11.
Divisibility by 12, 14, 15 –
Divisibility by numbers like 12, 14, 15 can be checked out by taking factors of the number which are relatively prime and checking the divisibility of the given number by each of the factors.
For example, a number is divisible by 12 if it is divisible both by 3 and 4.
Divisibility by 19 –
If the sum of the number of tens in the number and twice the units digit is divisible by 19, then the given number is divisible by 19. Otherwise it is not.
Take the units digit of the number, double it and add this figure to the remaining part of the number. If the result so obtained is divisible by 19, then the original number is divisible by 19. If that result is not divisible by 19. then the number is not divisible by 19.
For example, if we take 969, doubling the units digit gives 18 which when added to 96 gives a result of 114. Since 114 is divisible by 19, the number 969 is divisible by 19.
Factors and Co-Primes of a Number
Number of Factors of a Number
If N is a composite number such that N \( = a^p \cdot b^q \cdot c^r ….. \) where a, b, c are prime factors of N and p, q, r…. are positive integers, then the number of factors of N is given by the expression $$ (p+1) (q+1) (r+1)…. $$
For example : \( 140 = 2^2 \times 5^1 \times 7^1 \). Hence 140 has \( (2+1)(1+1)((1+1) = 12 \ factors \).
Please note that the figure arrived at by using the above formula includes 1 and the given number N also as factors. So if you want to find the number of factors the given number has excluding 1 and the number itself, we find out (p+1)(q+1)(r+1) and then subtract 2 from that figure.
In the above example, the number 140 has 10 factors excluding 1 and itself.
Number of ways of expressing a given number as a product of two factors
The given number N (which can be written as equal to \( a^p \cdot b^q \cdot c^r ….. \) where a, b, c are prime factors of N and p, q, r …… are positive integers) can be expressed as the product of two factors in different ways.
The number of ways in which this can be done is given by the expression- $$\frac{1}{2} {(p+1)(q+1)(r+1)…..} $$
For Example : 140 can be expressed as a product of two factors in \( \frac{12}{2} \) or 6 ways (because (p+1)(q+1)(r+1) in the case of 140 is equal to 12).
If p, q, r, ….. etc. are all even, then the product (p+1) (q+1)(r+1) ……. becomes odd and the above rule will not be valid since we cannot take \( \frac{1}{2} \) of an odd number to get the number of ways.
If p, q, r, … are all even, it means that the number N is a perfect square.
This situation arises in the specific cases of perfect squares because a perfect square can also be written as (square root x square root).
Thus, to find out the number of ways in which a perfect square can be expressed as a product of 2 factors, we have the following 2 rules –
as a product of two different factors :- $$ \frac{1}{2}{[(p+1) (q+1)(r+1)……-1] } ways$$ $$ (excluding \sqrt{N}\times\sqrt{N}) $$
as a product of two factors :- $$ 1/2{[(p+1)(q+1)(r+1)…….+1]} ways$$ $$(including \sqrt{N}\times\sqrt{N})$$
Sum of all the factors of a number
If a number N \( = a^p \cdot b^q \cdot c^r ….. \) where a, b, c….. are prime numbers and p, q, r….. are positive integers, then, the sum of all the factors of N (including 1 and the number itself) is: $${\LARGE(} \frac{a^{p+1}-1}{a-1} {\LARGE)} \cdot {\LARGE(} \frac{b^{q+1}-1}{b-1} {\LARGE)} \cdot {\LARGE(} \frac{c^{r+1} -1}{c-1} {\LARGE)} ….. $$
For Example : consider the number 48, when resolved into prime factors, \( 48=2^{4}\times3^{1} \) Here a=2, b=3, p=4, q=1 . Hence, sum of all the factors \( = (\frac{2^{4+1}-1}{2-1})(\frac{3^{1+1}-1}{3-1})=\frac{31}{1}\times\frac{8}{2}=124 \).
Number of ways of writing a number as product of two Co-Primes
If N\( = a^p \cdot b^q \cdot c^r ….. \) where a, b, c….. are prime numbers and p, q, r….. are positive integers, then, the number of ways of writing N as a product of 2 co-primes is – $$ 2^{n-1} $$ where ‘n’ is the number of distinct prime factors of the given number N.
For Example : If we take 48, which is \( 2^{4}\times3^{1} \) the value of ‘n’ is 2 because only two distinct prime factors (i.e. 2 and 3 only) are involved. Hence, the number of ways \( = 2^2-1=2^1= 2 \) i.e. 48 can be written as product of 2 co-primes, in two different ways. They are (1, 48) and (3, 16).
Number of co-primes to N, that are less than N
If N\( = a^p \cdot b^q \cdot c^r ….. \) where a, b, c….. are prime numbers and p, q, r….. are positive integers, then, the number of co-primes of N, which are less than N, represented by \( \phi \) (N) is – $$N{\LARGE(}1-\frac{1}{a}{\LARGE)}{\LARGE(}1-\frac{1}{b}{\LARGE)}{\LARGE(}1-\frac{1}{c}{\LARGE)} $$
For example : if 48 is considered, \( N=a^{p}.b^{q}. c^r ….. \) i.e. \( 48=2^{4}.3^{1} \). Hence, a=2 b=3 , p=4 q=1 \( \\ \phi (48) = 48{\LARGE(}1-\frac{1}{2}{\LARGE)}{\LARGE(}1-\frac{1}{3}{\LARGE)} = 48 \times \frac{1}{2} \times {2}{3} = 16 \)
Sum of co-primes to N that are less than N
The sum of the co-primes of N, that are less than N is – $$ {\LARGE(} \frac{N}{2} {\LARGE)} \cdot \phi (N) $$
For Example : if we consider the above example 48, we have \( \phi(48) = 16\) Hence, sum of co-primes of 48 that are less than 48 \( \\ ={\LARGE(} \frac{48}{2} {\LARGE)}\times 16 = 384 \)
Factors and Multiples of two or more Numbers
Least Common Multiple (LCM) and Highest Common Factor (HCF)
Least Common Multiple (LCM) –
The LCM of two or more numbers is the least number which is divisible by each of these numbers (i.e. leaves no remainder, or remainder is zero).
It is the expression of the lowest dimension which is divisible by each of them i.e. leaves no remainder, or remainder is zero.”
Highest Common Factor (HCF) –
The HCF is the largest factor of two or more given numbers.
It is the expression of highest dimension which divides each of them without remainder.
HCF is also called GCD (Greatest Common Divisor).
Important Points –
Product of two numbers = LCM × HCF
LCM is a multiple of HCF
For finding LCM and HCF of fractions, first reduce each fraction to its simplest form i.e., cancel out any common factors between the denominator and numerator and then apply appropriate formula from the following : $$HCF \ of \ fractions = \frac{HCF \ of \ numerator}{LCM \ of \ denominator} $$ $$ LCM \ of \ fractions = \frac{LCM \ of \ numerator}{HCF \ of \ denominator} $$
LCM and HCF can each be found by either one of two methods:
Factorization
Division \( \\ \) \( \\ \)
LCM by Factorization –
Resolve the numbers into prime factors. Then multiply the product of all the prime factors of the first number by those prime factors of the second number, which are not common to the prime factors of the first number.
This product is then multiplied by those prime factors of the third number, which are not common to the prime factors of the first two numbers.
In this manner, all the given numbers have to be dealt with and the last product will be the required LCM.
For Example : in order to find the LCM of 144, 504 and 720 we write each number in terms of its prime factors. \( \\144 = 3^2 \times 2^4\) \( \\ 504 = 3^2 \times 2^3 \times 7^1 \) \( \\ 720 = 2^4 \times 3^2 \times 5^1 \) \( \\ LCM \ is \ 24 \times 32 \times 7 \times 5 = 5040 \) \( \\ \) \( \\ \)
LCM by Division –
Select any one prime factor common to at least two of the given numbers. Write the given numbers in a line and divide them by the above prime number. Write down the quotient for every number under the number itself.
If any of the numbers is not divisible by the prime factor selected, write the number as it is in the line of quotients.
Repeat this process for the line of quotients until you get a line of quotients, which are prime to each other (i.e., no two “quotients” should have a common factor).
The product of all the divisors and the numbers in the last line will be the required LCM.
For Example : in order to find the LCM of 16, 9, 49 \( \\ \) \( \\ \) Thus, LCM = \( 2^3 \times 3^2 \times 1 = 72 \) \( \\ \) \( \\ \)
HCF by Factorization –
Resolve the given number into prime factors.
The product of the prime factors common to all the numbers will be the required HCF.
For Example : in order to find the HCF of 324, 576 and 784, first of all we resolve all the numbers into their prime factors \( 324 = 3^4 \times 2^2 \\ 576 =3^ 2 \times 2^6 \\ 784 = 7^2 \times 2^4 \) Then take the product of the factors common to all the numbers. HCF here will be \( 224 \). \( \\ \) \( \\ \)
HCF by Long Division –
Take two numbers. Divide the greater by the smaller, then divide the divisor by the remainder, divide the divisor of this division by the next remainder and so on until the remainder is zero.
The last divisor is the HCF of the two numbers taken.
In case of 3 numbers, by the same method find the HCF of any 2 numbers and then find the HCF of this HCF and the third number. This will be the HCF of the three numbers.
For Example in order to find the HCF of 242 and 34 \( \\ \) 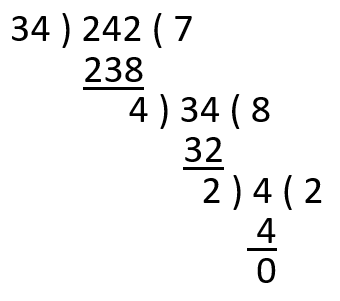\( \\ \) Hence HCF of 242 and 34 is 2.
LCM and HCF Models
LCM-Model 1 –
In this model of problem, you will need to find out the smallest number (or number in a specified range like the largest five-digit number) which when divided by 2 or more other numbers (i.e., divisors) leaves the same remainder in all cases.
General Rule : Any number which when divided by p, q or r leaving the same remainder “s” in each case will be of the form \( [ k \ (LCM \ of \ p, q \ and \ r) + s ] \) where k = 0, 1, 2, ….. If we take k = 0, then we get the smallest such number.
For Example : Find the smallest number which when divided by 5 or 8, leaves a remainder of 2 in each case and the number being greater than the two divisors. \( \\ \) The LCM of 5 and 8 is 40. Hence the required number is \( 40+2 = 42 \) \( \\ \) \( \\ \)
LCM-Model 2 –
In this model, the remainders in the divisions given will not be the same but the difference between the divisor and the remainder (i.e. the complement of the remainder) will be the same in each case.
General Rule : Any number which when divided by p, q or r leaving respective remainders of s, t and u where (p-s) = (q-1) = (r-u) = v (say), will be of the form \( [ k \ (LCM \ of \ p, q \ and \ r) – v ] \). The smallest such number will be obtained by substituting k = 1.
For Example : Find the smallest number which when divided by 19 and 23 leaves remainders of 13 and 17 respectively. \( \\ \) The LCM of 19 and 23 is 437. The difference between the divisor and the remainder in each case is the same i.e. (19-17 = 6) and (23-17 = 6). Hence, the number that satisfies the given conditions will be equal to \( 437-6=431 \). \( \\ \) \( \\ \)
HCF-Model 1 –
In this model, we have to identify the largest number that exactly divides the given dividends (which are obtained by subtracting the respective remainders from the given numbers).
General Rule : The largest number with which the numbers p, q or r are divided giving remainders of s, t and u respectively will be the HCF of the three numbers \( (p-s) (q-t) and (r-u) \).
For Example : Find the largest number with which when 425 and 373 are divided, respective remainders of 2 and 4 are left. \(\\ \) Since 425 when divided by the number gives a remainder of 2 it means (425-2 = 423) is exactly divisible by that number. Similarly (373-4 = 369) is also exactly divisible by that number. Thus, the required number is \( HCF \ of \ (369, 423) = 9 \). \( \\ \) \( \\ \)
HCF-Model 2 –
In this model, the problem will be as follows :- “Find the largest number with which if we divide the numbers p, q and r, the remainders are the same.”
General Rule : Take the difference between any two pairs out of the three given numbers. Let us say we take the two differences (p-q) and (p-r). The HCF of these numbers will be the required number. Here, the required number = HCF of \( (p-q) \ and \ (p-r) \) = HCF of \( (p-q) \ and \ (q-r) \) = HCF of \( (q-r) \ and \ (p-r) \).
For Example : Find the largest number with which when 472, 832 and 1372 are divided, the remainders are the same. \( \\ \) Take the difference between any two numbers out of the three given numbers \( \\ 832-472 = 360 \\ 1372-832 = 540 \) The required number is the HCF of these two differences i.e., \( HCF \ of \ (360, 540) = 180 \).
Successive Division
If the quotient of a division is taken and this is used as the dividend in the next division, such a division is called “successive division.”
A successive division process can continue up to any number of steps until the quotient in a division becomes zero for the first time. i.e., the quotient in the first division is taken as dividend and divided in the second division; the quotient in the second division is taken as the dividend in the third division; and so on.
Factorial
Factorial is first defined for positive integers. It is denoted by or “!”. Thus “Factorial n” is written as “n!”.
Factorial “n!” is defined the product of all the integers from 1 to n.
When any two consecutive integers are taken one of them is odd and the other is even. Hence the product of any two consecutive integers is always even i.e. divisible by 2.
Two consecutive integers can be written in the form of \( (n) \) and \( (n-1) \) or \( (n) \) and \( (n + 1) \). Hence, any number of the form \( n(n-1) \) or \( n(n+1) \) will always be even.
Out of any 3 consecutive integers, one of them is divisible by 3 and at least one of the three is definitely even. Hence, the product of any 3 consecutive integers is always divisible by 6.
Three consecutive integers can be of the form \( (n-1) , n \) and \( (n+1) \). The product of 3 consecutive integers will be of the form \( (n-1)n(n+1) \) or \( n(n^{2}-1) \) or \( (n^{3}-n) \). Hence any number of the form \( (n-1)n(n+1) \) or \( n(n^{2}-1) \) or \( (n^{3}-n) \) will always be divisible by 6.
Out of any n consecutive integers, exactly one number will be divided by n and the product of n consecutive integers will be divisible by n!
Any prime number greater than 3 can be written in the form of \( (6k+1) \) or \( (6k 1) \).
The Last digit of any Power
The last digits of the powers of any number follow a cyclic pattern i.e., they repeat after certain number of steps.
If we find out after how many steps the last digit of the powers of a number repeat, then we can find out the last digit of any power of any number.
For Example : Powers of 2 exhibit a pattern in their last digits.
The last digit of 21 is 2.
The last digit of 22 is 4.
The last digit of 23 is 8.
The last digit of 24 is 6.
The sequence then repeats: the last digit of 25 is the same as that of 21, and so on.
The last digit repeats every 4 steps for the powers of 2. Therefore, if the power is a multiple of 4, the last digit will be the same as the last digit of 24.
In order to find the last digit of 267, find the nearest multiple of 4 less than or equal to 67, which is 64. Thus, the last digit of 267 will be the same as the last digit of 23, which is 8.
Similarly, we can find the power cycle of all other numbers.
Last Digit of a Sum or Product
In general, when we want to find out the last digit of the sum of two numbers, we can just take the last digit of the two numbers and add them up. That will be the last digit of the sum.
Similarly, the last digit of a product will be equal to the last digit of the product of the last digits of the two given numbers.
Some Important Theorems
Binomial Theorem –
For any natural number \( n, (a + b)^n = ^{n}C_{0}a^{n} + ^{n}C_{1}a^{n-1}b + ^{n}C_2a^{n-2}b^{2} + ….. +^{n}C_{n-1}ab^{n-1}+^{n}C_{n}b^{n} \) where \( ^{n}C_r \) is the number of ways of choosing r objects out of n distinct objects and is given by – $$ ^{n}C_{r}=\frac{n(n-1)(n-2)…(n-r+1)}{1(2)(3)…(r)}=\frac{n!}{r!(n-r)!} $$ It can be observed that \( (a+b)^{n}=a^{n}+ \) (A multiple of b) \( = \) (A multiple of a) \( +b^{n} \). \( \\ \)
Fermat’s little theorem –
If p is prime and \( HCF (a, p)=1 \) then \( a^{p-1}-1 \) is a multiple of \( p \).
For example : take p = 5, a = 3. From the theorem, \( 3^{4}-1 \ or \ 80 \) is a multiple of 5.
If we take successive powers of 3, we get all the possible remainders. \( 3^{1}=3, 3^{2}=4, 3^{3}=2 , 3^{4}=1 \ (also \ 3^{5}=3 , 3^{6}=3^{2}, 3^{7}=3^{3} etc) \). At a certain stage, we get a remainder of 1 and after that, the pattern repeats. In this example, the pattern is 3, 4, 2, 1, 3, 4, 2,1 etc. The pattern length is 4. In general, it would be (p-1) or some factor of (p-1). \( \\ \)
Wilson’s Theorem –
If p is a prime, \( (p-1)! +1 \) is a multiple of p.
For Example : (2-1)! + 1 = 2(1), (3-1)! +1 = 3(1), (5-1)! + 1 = 5(1), and so on.
Rules Pertaining to \( a^{n}+b^{n} \ or \ a^{a}-b^{a} \)
Sometimes, there will be problems involving numbers. that can be written in the form \( a^{n}+b^{n} \ or \ a^{n}-b^{n} \) which can be simplified using simple rules. \( \\ \)
The following rules should be remembered for numbers in the form of \( a^{n}-b^{n} \) –
It is always (ie when n is even as well as odd) divisible by (a-b).
When n is even it is also divisible by (a+b).
When n is odd it is divisible by (a+b) if (a+b) is a factor of \( 2 \cdot b^{n} \). \( \\ \)
The following rules should be remembered for numbers in the form of \( a^{n}+b^{n} \) –
When n is odd it is divisible by (a+b).
When n is odd, it is divisible by (a-b) when (a-b) is a factor of \( 2 \cdot b^{n} \).
When n is even, it is divisible by (a+b) if (a+b) is a factor of \( 2 \cdot b^{n} \).
NUMBER SYSTEM
Base
Base is a number which decides the place value of a symbol or a digit in a number.
Alternatively, it is the number of distinct symbols that are used in that number system.
Note:
(A) The base of a number system can be any integer greater than 1.
(B) Base is also termed as radix or scale of notation.
Note :-
The base of a number system can be any integer greater than 1.
Base is also termed as radix or scale of notation.
The following table lists some number systems along with their respective base and symbols :- \( \\ \)
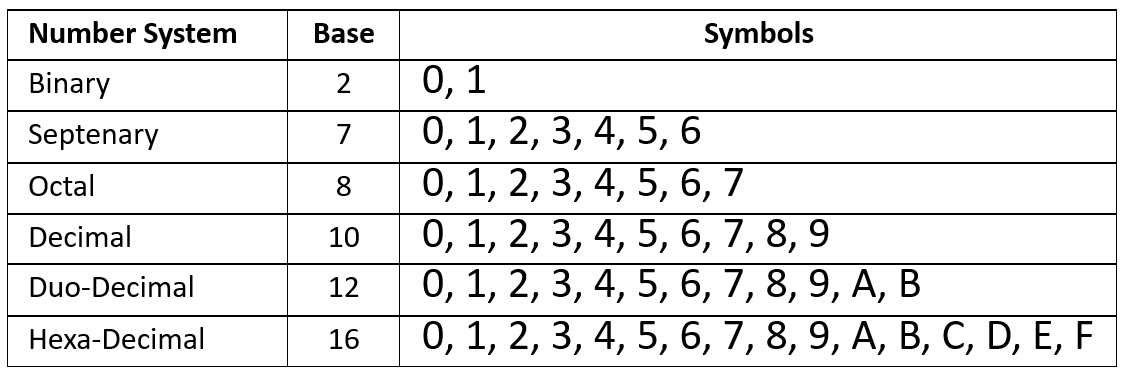
Note :- A=10, B=11, C =12, D=13, E=14, F=15 . Some may denote 10 as “E” and 11 as “e”.
Representation
Let N be any integer, r be the base of the system and let \( a_0 , a_1 , a_{2} ……… a_n \) be the required digits by which N is expressed., then – $$N=a_{n}r^{n}+a_{n-1}r^{n-1}+a_{n-2}r^{n-2}+ ………. + a_{1}r + a_{0} $$ where \( 0 \le a_{i} < r \) .
We will understand this by an example : \( (252)_{10}=(11111100)_{2} \) \( \\ \)
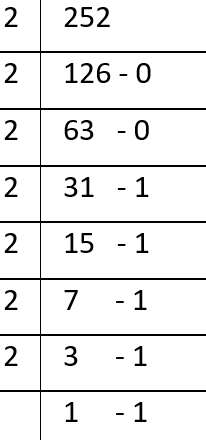
Note :- The remainders are written from bottom to top. \( \\ \)
Binary to Decimal –
We will understand this by an example : \( (101011001)_{2}=(345)_{10} \) \( \\ \) \( (101011001)_{2} =1 \times 2^{8}+ 0 \times 2^{7}+1\times 2^{6}+ 0 \times 2^{5} + 1 \times 2^{4} + 1 \times 2^{3}+0\times 2^{2}+0\times 2^{1}+1 \times 2^{0} \\ = 256+0+64+0+16+8+0+0+1 = (345)_{16} \) \( \\ \)
Decimal to Octal –
We will understand this by an example : \( (2593)_{10}=(5041)_{8} \) \( \\ \)
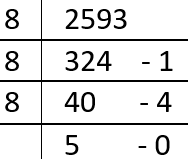
Note :- The remainders are written from bottom to top. \( \\ \)
Octal to Decimal –
We will understand this by an example : \( (3721)_{8}=(2001)_{10} \) \( \\ (3721)_{8}=3\times 8^{3}+7\times 8^{2}+2\times 8^{1}+1\times 8^{0} \\ =1536+448+16+1=(2001)_{10} \) \( \\ \)
Decimal to Hexa-decimal –
We will understand this by an example : \( (47236)_{10}=(B884)_{16} \) \( \\ \)
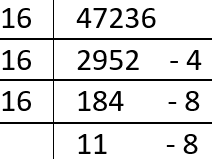
Note :- The remainders are written from bottom to top. \( \\ \)
Hexa-Decimal to Decimal –
We will understand this by an example : \( (51B)_{16}=(1307)_{10} \) \( \\ (51B)_{16} = 5 \times 16^{2} + 1 \times 16^{1} +B \times 16^{0} \\ = 1280 + 16 + 11 = (1307)_{10} \) \( \\ \)
Decimal to Duo Decimal or Duodenary (base 12) –
We will understand this by an example : \( (946)_{10}=(66A)_{12} \) \( \\ \)
Note :- The remainders are written from bottom to top. \( \\ \)
Duo-decimal to Decimal –
We will understand this by an example : \( (5BA)_{12}=(862)_{10} \) \( \\ (5BA)_{12}=5\times 12^{2}+B\times 12^{1}+A\times 12^{0} \\ =720+132+10=(862)_{10} \) \( \\ \)
Binary to Octal –
8 being the base of octal system and 2 being the base of binary system, there is a close relationship between both the systems. One can just club three digits of a binary number into a single block and write the decimal equivalent of each group (left to right).
We will understand this by an example : \( (100101011)_{2}=(100)_{2} \ (101)_{2} \ (011)_{2}=(453)_{8} \\ \therefore (100101011)_{2}=(453)_{8} \) \( \\ \)
Binary to Hexa-Decimal –
This is similar to the method discussed for octal; instead of clubbing 3, we club 4 digits.
We will understand this by an example : \( (10101110)_{2}=(1010)_{2} \ (1110)_{2}=(10)(14)=(AE)_{16} \\ (10101110)_{2}=(AE)_{16} \) \( \\ \)
\( \\ \) Thus, LCM = \( 2^3 \times 3^2 \times 1 = 72 \) \( \\ \) \( \\ \)
\( \\ \) Hence HCF of 242 and 34 is 2.
