Profit, Loss & Partnership – Concepts for Aptitude

1. The Selling Price (SP) and Cost Price (CP)of an article determines the profit or loss made on the particular transaction. Some basic formulas are as follows:

Profit

Profit = SP – CP

Profit % = $\frac{Profit}{CP} *100$

$SP = CP{\LARGE[}1+\frac{P\%}{100}{\LARGE]} \Longrightarrow \ CP = SP{\LARGE[}\frac{100}{100+P\%}{\LARGE]}$

Loss

Loss = CP – SP

Loss% = $\frac{Loss}{CP} *100$

$SP = CP{\LARGE[}1-\frac{L\%}{100}{\LARGE]}\Longrightarrow \ CP = SP{\LARGE[}\frac{100}{100-L\%}{\LARGE]}$

Q: A shopkeeper buys oranges at 100 and sells it at 120 per kg. How much profit or loss does he make on every kg and in percentage terms?

Sol: Profit on 1 kg = SP – CP = 120 – 100 = 20

Profit % = 20/100 = 20%

Q: A student purchased Aptitude book for Rs 700 but did not study it at all. He had to sell it at a loss of 20% as there we not many buyers. What was his selling price?

Sol: Profit on 1 kg = SP – CP = 120 – 100 = 20

$SP = 700*{\LARGE[}1-\frac{20\%}{100}{\LARGE]} = 560$

2. When two articles are sold at the same price (i.e their SP is the same) such that there is a Profit of x% on one article and a Loss of x% on the other:

Then, irrespective of what the CP actually is, the net resultant of the transaction is Loss.

Overall loss can be calculated as: (no need to memorize but you should know how to work with such problems)

$Loss\% =\frac{x^2}{100} = {\LARGE[}\frac{x}{10}{\LARGE]}^2$

Q: Anita sold two different products at same selling price of 250 on amazon, but one at a loss of 10% and another at a profit of 10%. What was her overall profit or loss percentage?

Sol: $Loss\% =\frac{10^2}{100} = 1%$

$SP = 700*{\LARGE[}1-\frac{20\%}{100}{\LARGE]} = 560$

3. when selling and cost price of a good is equated in terms of quantities of articles sold. In that case, profit can also be calculated without taking into account their SP or CP. One such method is: (no need to memorize)

Profit% = $\frac{Goods Left}{Goods Sold}*100 $

Q. A Seller recovers the cost of 25 shoes by selling 20 shoes. Calculate the profit percentage.

Sol: Profit% = $\frac{Goods Left}{Goods Sold}*100$

$= \frac{(25-20)}{20}*100=25\%$

Note: You can solve this problem by basics as follow:

Alternative Sol: Assume selling price = 100

SP of 20 shoes = 2000 = CP of 25 shoes

CP of 1 shoe = 2000/ 25 = 80

Profit = (100-80) = 20

Profit % = 20/80*100 = 25%

4. Marked Price (List Price), Selling Price, Discount, Cost Price and Profit:

It’s very simple concept. Go to amazon or Myntra and look for any item on discount, you will see price like below:

In the following example of a shoe:

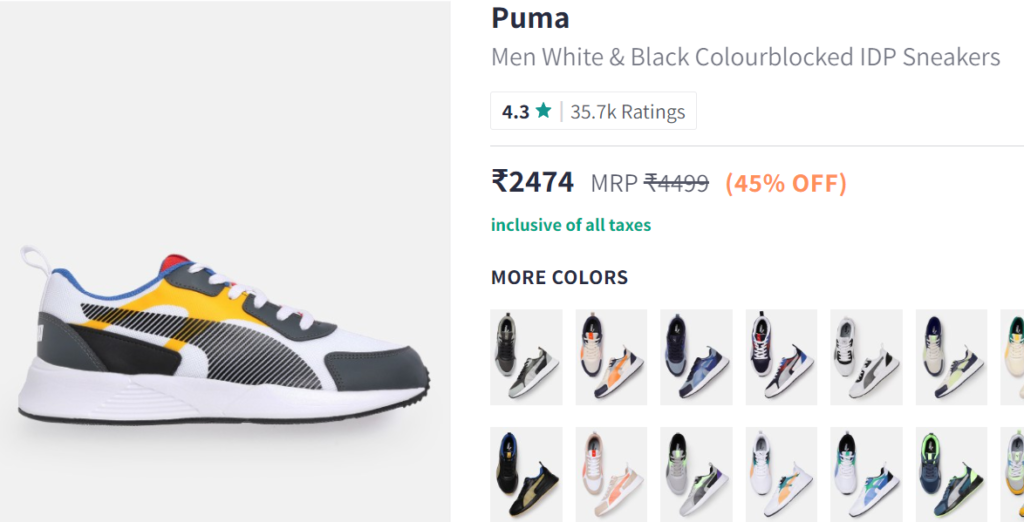
Marked Price is 4499/- (which is the MRP)
Selling Price is 2474/- (which is the price at which they are selling it on website)
Discount is 45% (because giving discount of 45% on MRP 4499 will give you the selling price of 2474)

Cost price is the price at which seller is purchasing it, which we don’t know about from the website. But if seller is purchasing it at below 2474, he is making a profit. If he is purchasing it above 2474, then he is making a loss. We are sure he is making a profit, otherwise why would they sell it 😛

Assume he is purchasing it at 2000, then his profit or mark up would be: (2474-2000) = 474
And Mark up % = 474/2000*100 = 23.7%

Now the boring formulas to what we just saw:

Markup

Markup = MP – CP
Markup% = $\frac{(MP – CP)}{CP} * 100$

Discount

If product is normally sold at Market Price then, SP = MP (or say 0% discount)
If product is sold at a Discounted Price on the Marked Price the, SP = MP – Discount
Discount = MP – SP
Discount% = $\frac{Discount}{MP}*100$

5. Successive Discount

If successive discounts are p%, q%, r% and so, on a product then the effective price after all these discounts is – $SP = MP*{\LARGE[}1-\frac{p}{100}{\LARGE]}{\LARGE[}1-\frac{q}{100}{\LARGE]}{\LARGE[}1-\frac{r}{100}{\LARGE]}$

Q: Lifestyle is offering a 20% discount on a shirt marked at ₹1,200. What is the selling price after the discount?

Sol: Discount = 20% of 1200 = ₹240

Selling Price = Marked Price – Discount = ₹1200 – ₹240 = ₹960

Q: Urban Ladder buys a sofa for ₹20,000 and marks it up by 25%. However, store gives a 30% discount on the marked price. What is his loss or profit?

Sol: Markup = 25%×20000 = ₹ 5000

Marked Price = ₹20000 + ₹5000 = ₹25000

Discount = 30%×25000= ₹7500

Selling Price = ₹25000 – ₹7500 = ₹17500

Loss = Cost Price – Selling Price = ₹20000 – ₹17500 = ₹2500

Q: Croma offers a 20% discount on a laptop marked at ₹60,000. After that, there’s an additional 10% discount. What is the final selling price?

Sol: First Discount = 20%×60000 = ₹12000

Price after first discount = ₹60000 – ₹12000 = ₹48000

Second Discount = 10%×48000 = ₹4800

Final Selling Price = ₹48000 – ₹4800 = ₹43200

Partnership (no need to memorize, just understand the basics of it)

6. Profit Sharing in Simple Partnership

When partners invest for the same period, profits are shared in proportion to their investments. It’s simple, if you invest more money, you will get more profit.

Q. A and B invest ₹20,000 and ₹30,000 respectively in a business for a year. At the end of the year, the business made a profit of ₹25,000. What is A’s share of the profit?

Sol: Total Investment = ₹20,000 (A) + ₹30,000 (B) = ₹50,000

A’s Share of profit = (20000/50000) * 25000 = 10000

B’s Share of profit = (30000/50000) * 25000 = 15000

7. Profit Sharing in Time-Based Partnership

When partners invest for different time periods, profits are shared based on both investment and the duration of investment. Since someone’s money is invested for longer, he should get more share of the profit.

Q. X and Y start a business together. X invests ₹50,000, and Y invests ₹40,000. X remains in the business for 12 months, and Y stays for 8 months. If the total profit is ₹36,000, how will the profit be shared?

Sol: X’s investment = ₹50,000 for 12 months, so X’s total contribution = 50,000×12 = 600,000

Y’s investment = ₹40,000 for 8 months, so Y’s total contribution = 40,000×8 = 320,000

Total contribution = 600,000+320,000 = 920,000

X’s share of the profit: (600,000 / 920,000) * 36,000 = ₹23,478

Y’s share of the profit: (320,000 / 920,000) * 36,000 = ₹12,522

Q: P and Q start a business by investing ₹60,000 and ₹90,000, respectively. After 6 months, R joins the partnership with ₹1,20,000. If the profit at the end of the year is ₹88,000, what will be the share of each partner?

Sol: P’s total investment contribution = 60,000×12= 720,000

Q’s total investment contribution = 90,000×12 = 1,080,000

R’s total investment contribution (since R was there for only 6 months) = 1,20,000×6 = 720,000

Total contribution = 720,000+1,080,000+720,000 = 2,520,000

P’s share of the profit: (720,000 / 2,520,000) * 88,000 = ₹25,143

Q’s share of the profit: (1,080,000 / 2,520,000) * 88,000 = ₹50,286

R’s share of the profit: (720,000 / 2,520,000) * 88,000 = ₹25,143

You can also refer following videos to get more perspective on the topic:

Practice

Refer Topic: Average, Mixture, Alligations: https://www.learntheta.com/placement-aptitude-average-mixture-alligation/

Refer more Aptitude Questions with Solutions on Profit and Loss: https://www.learntheta.com/aptitude-questions-profit-loss-partnership/

Practice Aptitude Questions on Profit and Loss with LearnTheta’s AI Practice Platform: https://www.learntheta.com/placement-aptitude/