Mensuration – Important Formulas and Concepts for Placement Aptitude
Basics
- Mensuration is the branch of geometry that deals with the measurement of length, area and volume. Key terms used in mensuration are briefly explained below :-
- Length: The measurement of the longest side of a geometric figure.
- Area: The measure of the space enclosed by a geometric figure.
- Volume: The measure of the space occupied by a three-dimensional figure.
- Surface Area: The total area of the surface of a three-dimensional figure.
- Perimeter: The total distance around the boundary of a two-dimensional figure.
Triangles
- The area of a triangle is represented by the symbol A. For any triangle, the lengths of the three sides are represented by a, b and c and the angles opposite these sides are represented by A, B and C respectively.
- For any triangle in general –
- when the lengths of three sides a, b, c are given, \( \\ \) \(Area = \sqrt{s(s-a)(s-b)(s-c)} \\ \) where, \( s=\frac{a+b+c}{2}=\frac{p}{2} \) (This is called Heron’s formula.)
- when base (b) and altitude (height) to that base are given, \( \\ Area = \frac{1}{2} (base)(altitude)=\frac{1}{2}bh \)
- For a right angled triangle –
- \( Area =\frac{1}{2}(Product \ of \ the \ sides \ containing \ the \ right \ angle) \\ \hspace{1cm} = \frac{1}{2}(base)(perpendicular) \)
- For an equilateral triangle –
- \( Area = \frac{\sqrt{3}a^{2}}{4} \) where, “a” is the side of the triangle \( \\ \) The height of an equilateral triangle \( =\frac{\sqrt{3}a}{2} \)
Quadrilaterals
- For any quadrilateral –
- \( Area \ of \ the \ quadrilateral = \frac{1}{2}(One \ diagonal) (Sum \ of \ the \ offsets \ drawn \ to \ that \ diagonal) \\ \) For the given figure, Area of quadrilateral (ABCD) \( = \frac{1}{2} (AC)(BE + DF) \\ \)
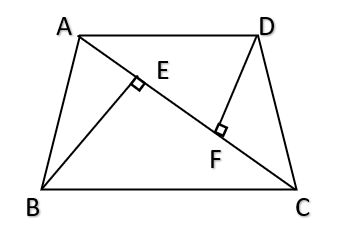
- \( Area \ of \ the \ quadrilateral = \frac{1}{2}(One \ diagonal) (Sum \ of \ the \ offsets \ drawn \ to \ that \ diagonal) \\ \) For the given figure, Area of quadrilateral (ABCD) \( = \frac{1}{2} (AC)(BE + DF) \\ \)
- For a trapezium –
- \( Area \ of \ a \ trapezium = \frac{1}{2}(Sum \ of \ parallel \ sides) (Distance \ between \ them) \\ \) For the given figure, \( Area = \frac{1}{2}(AD+BC)(AF) \\ \)
- \( Area \ of \ a \ trapezium = \frac{1}{2}(Sum \ of \ parallel \ sides) (Distance \ between \ them) \\ \) For the given figure, \( Area = \frac{1}{2}(AD+BC)(AF) \\ \)
- For a parallelogram –
- \( Area = (Base) \times (Height) \) \( \\ \)
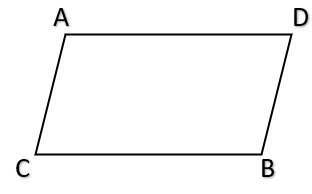
- \( Area = (Base) \times (Height) \) \( \\ \)
- For a rhombus –
- \( Area =\frac{1}{2} (Product \ of \ the \ diagonals) \\ \hspace{1cm} = \frac{1}{2}(d_{1} \times d_{2}) \)
- \( Perimeter = 4(Side \ of \ the \ rhombus) \) \( \\ \)
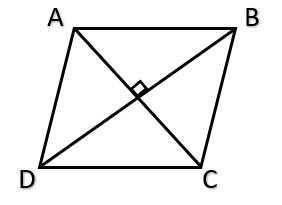
- For a rectangle –
- \( Area = (Length)(Breadth) = lb \)
- \( Perimeter = 2(l+b) \) , where l and b are the length and the breadth of the rectangle respectively \)
- \( Diagonal (d) = \sqrt{l^2+b^2} \) \( \\ \)
- For a square –
- \( Area = (Side)^2 \)
- \( Area = \frac{1}{2} (Diagonal)^2 \)
- \( Perimeter = 4(Side) \)
- \( Diagonal = \sqrt{2} (side) \) \( \\ \)
Circle
- \( Area \ of \ the \ circle = ar² \) where, r is the radius of the circle.
- \( Circumference = 2 \pi г \)
- \( Sector \ of \ a \ circle \ = Length \ of \ arc = \frac{\theta}{360°}(2πг) \\ Area = \frac{\theta}{360°}(πr^2) \) where \( \theta \) is the angle of the sector in degrees and r is the radius of the circle.
- \(Area = (1/2)Ir \) where, l is length of arc and r is radius.
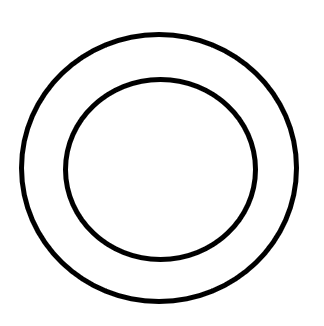
- Ring – Ring is the space enclosed by two concentric circles. \( \\ Area = \pi R^2 – \pi r² = \pi (R+r)(R-r) \) where, R is the radius of the outer circle and r is the radius of the inner circle. \( \\ \)
Area and Volume of Solids
Solids are three-dimensional objects which, in addition to area, have volume also. For solids, two different types of areas are defined
Lateral surface area or curved surface area – lateral surface area is the area of the lateral surfaces of the solid.
Total surface area – Total surface area includes the areas of the top and the bottom surfaces also of the solid. Hence, Total surface area = Lateral surface area + Area of the top face + Area of the bottom face.
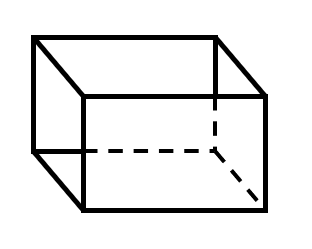
Cuboid
- A right prism whose base is a rectangle is called a cuboid or rectangular solid.
- If a and b are respectively the length and breadth of the base and h, the height of the prism, then –
- \( Volume = lbh \)
- \( Lateral \ Surface \ Area = 2(l+ b)h \)
- \( Total \ Surface \ Area = 2(l + b)h + 2lb\) \( \ = 2(lb + lh + bh) \)
- \( Longest \ diagonal \ of \ the \ cuboid = \sqrt{l² + b² +h²} \) \( \\ \)
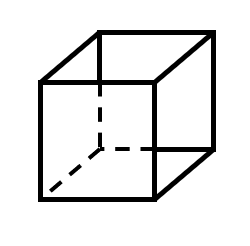
Cube
- A right prism whose base is a square and height is equal to the side of the base is called a cube.
- If a is the edge of the cube, then –
- \( Volume = a³\)
- \( Lateral \ Surface \ Area = 4a^2 \)
- \( Total \ Surface \ Area = 6a^2 \)
- \( Diagonal \ of \ the \ cube = a \sqrt{3} \) \( \\ \)
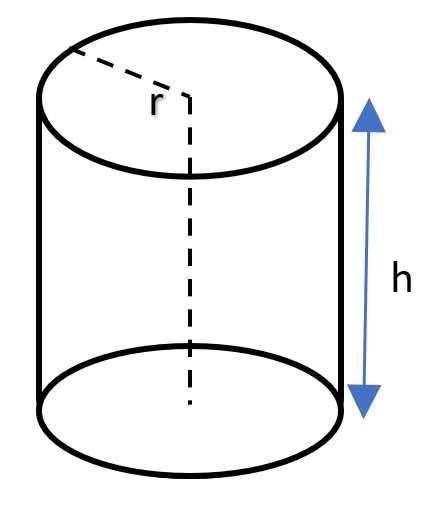
Cylinder
- A cylinder is equivalent to a right prism whose base is a circle.
- A cylinder has a single curved surface as its lateral faces.
- If r is the radius of the base and h is the height of the cylinder, then –
- \( Volume = r²h \)
- \( Curved \ Surface \ Area = 2\pi rh \)
- \( Total \ Surface \ Area = 2 \pi rh+ 2 \pi r² \) \( \ = 2 \pi r(h + r) \) \( \\ \)
- A hollow cylinder has a cross-section of a ring.
- Volume of the material contained in a hollow cylindrical shell \( = \pi (R^2 – r^2)h \) where, R is the outer radius, r is the inner radius and h the height.
Pyramid
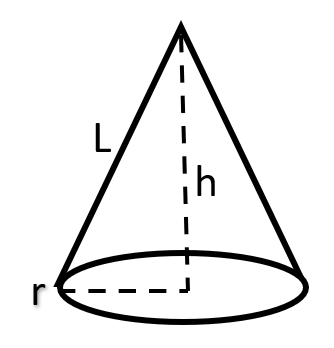
Cone
- A cone is equivalent to a right pyramid whose base is a circle.
- The lateral surface of a cone does not consist of triangles like in a right pyramid but is a single curved surface.
- If r is the radius of the base of the cone, h is height of the cone and I is the slant height of the cone, then –
- \( l^{2} = r^{2}+h^{2} \)
- \( Volume = \frac{1}{3} \pi r^{2}h \)
- \( Curved \ Surface \ Area = \pi rl \)
- \( Total \ Surface \ Area = \pi rl+\pi r^2 \) \( \ = \pi r (l+r) \) \( \\ \)
Sphere
- A sphere is a three-dimensional geometric object that is perfectly round in shape.
- It is defined as the set of all points in space that are equidistant from a given point called the center.
- If r is the radius of the sphere, then –
- \( Volume = \frac{4}{3} \pi г^3 \)
- \( Surface \ Area = 4 \pi r^2 \)
- The of a hemisphere is equal to half the surface area of a sphere, i.e.,
Hemisphere
- A hemisphere is a three-dimensional geometric shape that is half of a sphere.
- It is formed by cutting a sphere along a plane passing through its center. This results in two equal parts, each resembling half of a sphere.
- If r is the radius of a hemisphere, then –
- \( Volume = \frac{2}{3} \pi г^3 \)
- \( Curved \ Surface \ Area= 2\pi r^{2} \).
You can also refer following videos to grasp basics in more details
Refer Topic: Ratio and Proportion: https://www.learntheta.com/placement-aptitude-ratio-proportion/
Read more about LearnTheta’s AI Practice Platform: https://www.learntheta.com/placement-aptitude/