Class 9 Maths: Ch 2 – Ploynomials – Extra Questions with Answers
Q. 1 If $p(x) = x^3 – 5x^2 + 4x – 2$ and $g(x) = x – 2$, find the remainder when $p(x)$ is divided by $g(x)$.
Check Solution
Ans: D
Solution: Use the Remainder Theorem. The remainder when $p(x)$ is divided by $x-2$ is $p(2)$.
$p(2) = (2)^3 – 5(2)^2 + 4(2) – 2 = 8 – 20 + 8 – 2 = -6$.
Answer: -6
Q. 2 Find the remainder when $x^3 – 2x^2 + 6x – 2$ is divided by $x – 2$.
Check Solution
Ans: C
Solution:
By the Remainder Theorem, the remainder is $P(2)$.
$P(2) = (2)^3 – 2(2)^2 + 6(2) – 2 = 8 – 8 + 12 – 2 = 10$.
Answer: 10
Q. 3 Factorise: $16a^2 – 24ab + 9b^2$
Check Solution
Ans: B
Solution:
$(4a)^2 – 2(4a)(3b) + (3b)^2$
$(4a – 3b)^2$
Answer: $(4a – 3b)^2$
Q. 4 Find $q(-1)$, $q(2)$, and $q(0)$ for the polynomial $q(x) = 5x^2 – 2x + 1$.
Check Solution
Ans: A
Solution:
$q(-1) = 5(-1)^2 – 2(-1) + 1 = 5 + 2 + 1 = 8$
$q(2) = 5(2)^2 – 2(2) + 1 = 20 – 4 + 1 = 17$
$q(0) = 5(0)^2 – 2(0) + 1 = 0 – 0 + 1 = 1$
Answer: $q(-1) = 8, q(2) = 17, q(0) = 1$
Q. 5 If $q(x) = x^2 – 3x + 2$, then $q(3)$ is equal to ______.
Check Solution
Ans: D
Solution: Substitute $x=3$ into the expression for $q(x)$.
$q(3) = (3)^2 – 3(3) + 2 = 9 – 9 + 2 = 2$.
Answer: 2
Q. 6 Which of the following is a factor of $(a+b)^3 – (a^3 + b^3)$?
Check Solution
Ans: A
Solution:
$(a+b)^3 – (a^3 + b^3) = a^3 + 3a^2b + 3ab^2 + b^3 – a^3 – b^3 = 3a^2b + 3ab^2 = 3ab(a+b)$.
Factors are 3, a, b, (a+b).
Answer: 3
Q. 7 Using the remainder theorem, find the remainder when $p(x) = 3x^3 – 8x^2 + 7x – 11$ is divided by $g(x) = x – 2$.
Check Solution
Ans: A
Solution:
By the Remainder Theorem, the remainder when $p(x)$ is divided by $x-2$ is $p(2)$.
$p(2) = 3(2)^3 – 8(2)^2 + 7(2) – 11 = 3(8) – 8(4) + 14 – 11 = 24 – 32 + 14 – 11 = -5$
Answer: -5
Q. 8 Use the Factor Theorem to determine whether g(x) is a factor of p(x): \(p(x) = 3x^3 – 4x^2 – 5x + 2\), \(g(x) = x – 2\)
Check Solution
Ans: D
Solution:
By the Factor Theorem, g(x) is a factor of p(x) if p(2) = 0.
p(2) = 3(2)^3 – 4(2)^2 – 5(2) + 2 = 3(8) – 4(4) – 10 + 2 = 24 – 16 – 10 + 2 = 0.
Answer: Yes
Q. 9 One of the factors of $(x+3y)^3 + (3x-z)^3 – (x+3z)^3 + 3(x+3y)(3x-z)(x+3z)$ is:
Check Solution
Ans: B
Solution:
Let $A = x+3y$, $B = 3x-z$, $C = x+3z$. The expression becomes
$A^3 + B^3 – C^3 + 3ABC$.
We can rewrite this as $A^3 + B^3 + (-C)^3 – 3A B (-C)$.
If $A+B-C = 0$, then $A^3 + B^3 + (-C)^3 – 3A B (-C) = A^3+B^3+(-C)^3-3AB(-C)=(A+B+(-C))(A^2+B^2+(-C)^2-AB-B(-C)-A(-C))=(A+B-C)(A^2+B^2+C^2-AB+BC+AC)$
We have $A+B-C = x+3y+3x-z-(x+3z) = 3x+3y-4z$.
However, if we let $A+B-C=0$, the expression is zero. Then we consider the identity $a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)$. In our case, we have $a^3+b^3+(-c)^3-3ab(-c)=(a+b-c)(a^2+b^2+c^2-ab+bc+ac)$.
We have the expression $A^3 + B^3 – C^3 + 3ABC$.
Let $A = x+3y, B = 3x-z, C = x+3z$. Then the given expression is $A^3+B^3-C^3+3ABC$.
$A^3+B^3-C^3+3ABC = A^3+B^3+(-C)^3-3AB(-C)$.
If $A+B+(-C) = 0$, then the expression is zero.
$A+B-C = x+3y+3x-z-(x+3z) = 3x+3y-4z$.
Let us consider the expression $(A+B-C)(A^2+B^2+C^2-AB+BC+AC)$. We can consider the case $A+B-C = 0$, which is equivalent to $3x+3y-4z=0$.
Now consider the expression $(A+B-C)(A^2+B^2+C^2-AB+AC+BC)$.
We have $A+B-C = x+3y+3x-z-(x+3z) = x+3y+3x-z-x-3z = 3x+3y-4z$.
$A+B-C = 3x+3y-4z$.
Also consider the expression $A^3 + B^3 – C^3 + 3ABC = (A+B-C)(A^2+B^2+C^2-AB+AC+BC)$.
$A+B-C = x+3y+3x-z-(x+3z) = 3x+3y-4z$.
If $3x+3y-4z = 0$, the expression is zero.
However, the problem asks for a factor.
$A^3 + B^3 – C^3 + 3ABC = (A+B)^3 – 3AB(A+B) – C^3 + 3ABC = (A+B)^3 – C^3 – 3AB(A+B-C)$
$A^3+B^3+(-C)^3-3AB(-C)=(A+B-C)(A^2+B^2+C^2-AB+AC+BC)$
$A+B+C = x+3y+3x-z+x+3z = 5x+3y+2z$
$A^3+B^3-C^3+3ABC = (x+3y+3x-z-(x+3z))(\dots)$
$= (3x+3y-4z) \dots$
$A^3 + B^3 – C^3 + 3ABC$
$A+B-C = x+3y+3x-z-x-3z = 3x+3y-4z$
If $x+3y+3x-z+x+3z \neq 0$
$(A+B-C) = 3x+3y-4z$
Answer: 3x+3y-4z
Q. 10 What is the first degree expression to be subtracted from $x^6 + 8x^4 + 2x^3 + 16x^2 + 4x + 6$ in order to make it a perfect square?
Check Solution
Ans: A
Solution:
Let the perfect square be $(x^3 + ax + b)^2$. Expanding this, we get $x^6 + 2ax^4 + 2bx^3 + a^2x^2 + 2abx + b^2$.
Comparing coefficients, we have:
$2a = 8 \implies a = 4$
$2b = 2 \implies b = 1$
Then the perfect square is $x^6 + 8x^4 + 2x^3 + 16x^2 + 8x + 1$.
The given expression is $x^6 + 8x^4 + 2x^3 + 16x^2 + 4x + 6$.
Subtracting the perfect square from the given expression:
$(x^6 + 8x^4 + 2x^3 + 16x^2 + 4x + 6) – (x^6 + 8x^4 + 2x^3 + 16x^2 + 8x + 1) = -4x + 5$.
The first degree expression is $-4x+5$.
Answer: $-4x+5$
Next Topic: Coordinate Geometry
Practice Extra Questions for Class 9 Maths
Build Strong Concepts for Maths & Science – with LearnTheta’s AI-Practice!
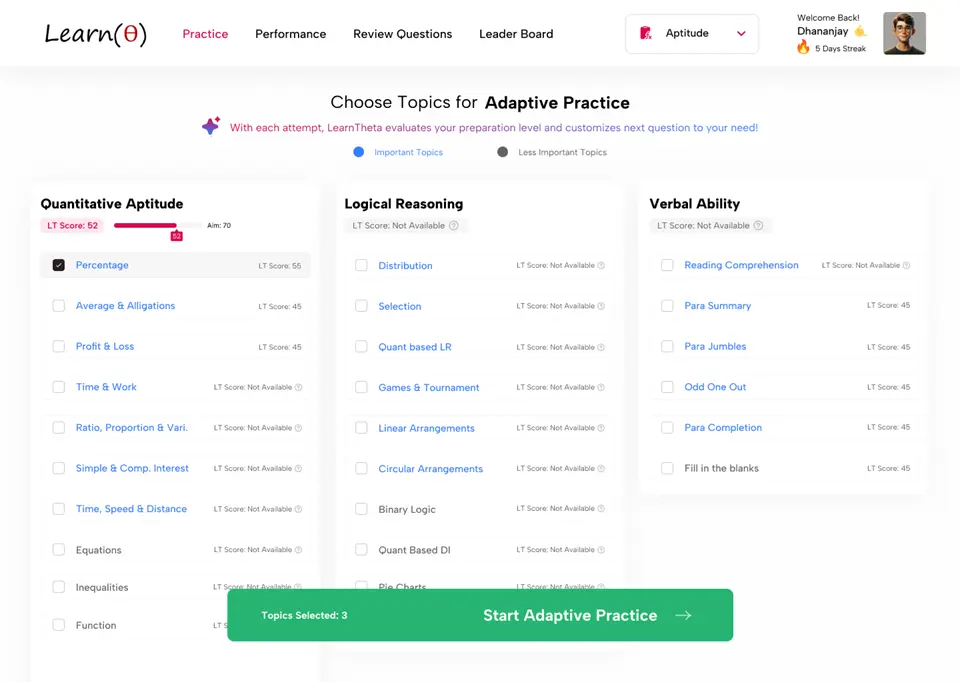
✅ All Topics at One Place
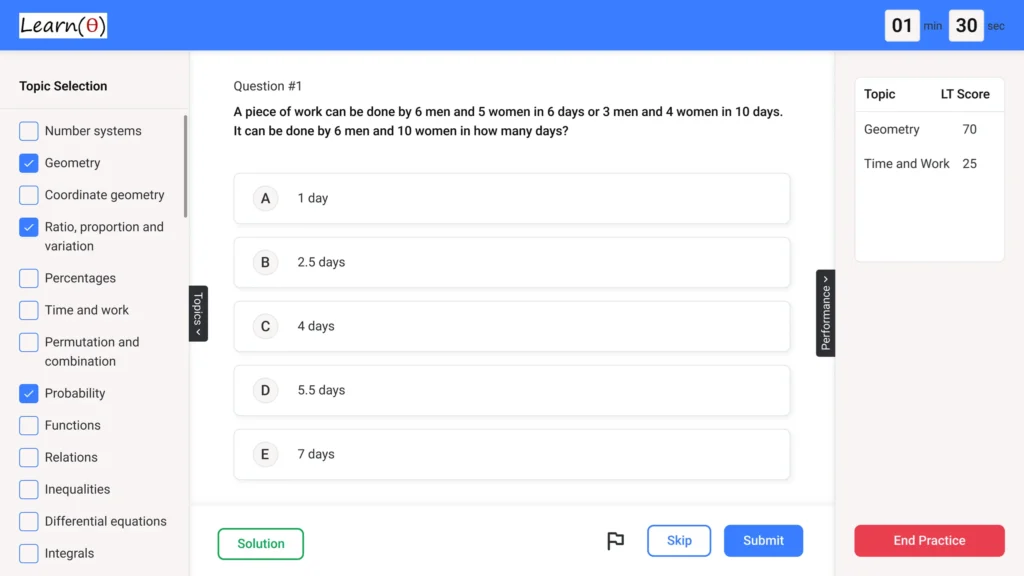
🤖 Adaptive Question Practice
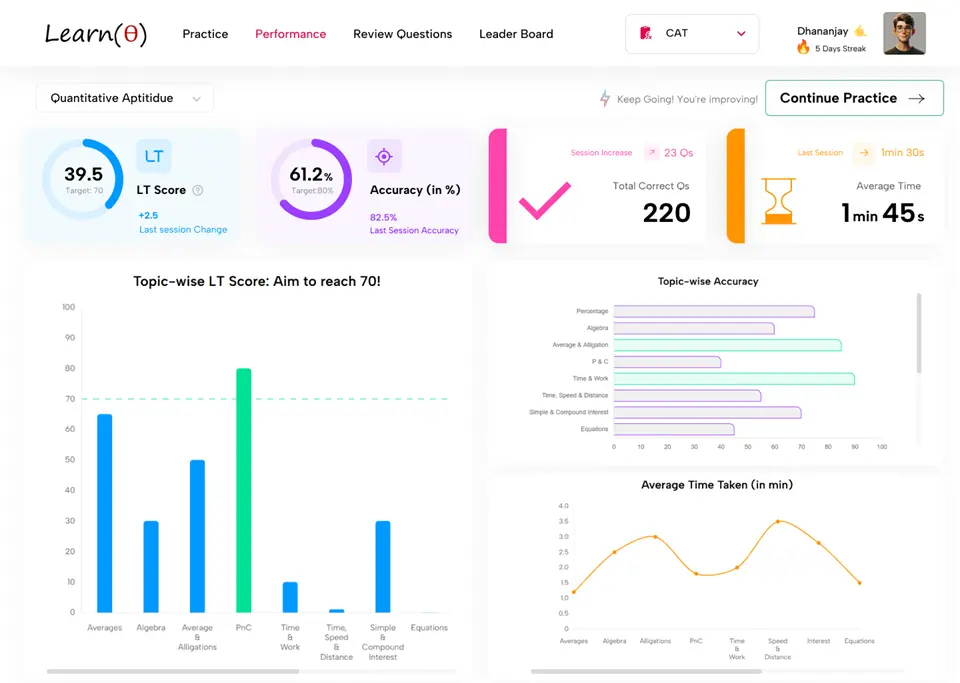
📊 Progress and Insights