Class 9 Maths: Ch 1 – Number Systems – Extra Questions with Answers
Q. 1 Insert a rational and an irrational number between 2.1 and 2.2.
Check Solution
Ans: C
Solution:
Answer: 2.15, √4.45
Q. 2 Express `3.\overline{7}` in the form `p/q`, where p and q are integers and q ≠ 0.
Check Solution
Ans: D
Solution:
Let x = 3.777…
Then 10x = 37.777…
Subtracting the first equation from the second, we get:
9x = 34
x = 34/9
Answer: 34/9
Q. 3 The number obtained on rationalising the denominator of $\frac{1}{\sqrt{5} – 1}$ is ______ .
Check Solution
Ans: C
Solution: Multiply the numerator and denominator by the conjugate of the denominator, which is $\sqrt{5} + 1$.
$\frac{1}{\sqrt{5} – 1} \times \frac{\sqrt{5} + 1}{\sqrt{5} + 1} = \frac{\sqrt{5} + 1}{5 – 1} = \frac{\sqrt{5} + 1}{4}$
Answer: $\frac{\sqrt{5}+1}{4}$
Q. 4 Find the value of $x$: $\sqrt[4]{4x-3} = 3$
Check Solution
Ans: A
Solution:
Raise both sides to the power of 4:
$(\sqrt[4]{4x-3})^4 = 3^4$
$4x-3 = 81$
$4x = 84$
$x = 21$
Answer: 21
Q. 5 Simplify the following: $\frac{\sqrt{12}}{6} + \frac{\sqrt{75}}{15}$
Check Solution
Ans: D
Solution:
$\frac{\sqrt{12}}{6} + \frac{\sqrt{75}}{15} = \frac{\sqrt{4 \cdot 3}}{6} + \frac{\sqrt{25 \cdot 3}}{15} = \frac{2\sqrt{3}}{6} + \frac{5\sqrt{3}}{15} = \frac{\sqrt{3}}{3} + \frac{\sqrt{3}}{3} = \frac{2\sqrt{3}}{3}$
Answer: $\frac{2\sqrt{3}}{3}$
Q. 6 Rationalize the denominator of: $\frac{20}{\sqrt{26} – 1}$
Check Solution
Ans: C
Solution: Multiply the numerator and denominator by the conjugate of the denominator, which is $\sqrt{26} + 1$.
$\frac{20}{\sqrt{26} – 1} \cdot \frac{\sqrt{26} + 1}{\sqrt{26} + 1} = \frac{20(\sqrt{26} + 1)}{26 – 1} = \frac{20(\sqrt{26} + 1)}{25} = \frac{4(\sqrt{26} + 1)}{5}$
Answer: $\frac{4(\sqrt{26} + 1)}{5}$
Q. 7 If $x = 14 + 6\sqrt{5}$, find the value of $\sqrt{x} + \frac{1}{\sqrt{x}}$.
Check Solution
Ans: D
Solution:
We have $x = 14 + 6\sqrt{5} = 9 + 6\sqrt{5} + 5 = (3+\sqrt{5})^2$.
Then $\sqrt{x} = \sqrt{(3+\sqrt{5})^2} = 3+\sqrt{5}$.
So $\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}} = \frac{3-\sqrt{5}}{(3+\sqrt{5})(3-\sqrt{5})} = \frac{3-\sqrt{5}}{9-5} = \frac{3-\sqrt{5}}{4}$.
$\sqrt{x} + \frac{1}{\sqrt{x}} = 3+\sqrt{5} + \frac{3-\sqrt{5}}{2} = \frac{6+2\sqrt{5}+3-\sqrt{5}}{2} = \frac{9+\sqrt{5}}{2}$.
We made an error. We have $14+6\sqrt{5} = 9+5+2(3)(\sqrt{5}) = (3+\sqrt{5})^2$.
So $\sqrt{x} = 3+\sqrt{5}$.
$\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}} = \frac{3-\sqrt{5}}{9-5} = \frac{3-\sqrt{5}}{4}$
$\sqrt{x} = 3+\sqrt{5}$ and $\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}}$.
$\sqrt{x} + \frac{1}{\sqrt{x}} = 3+\sqrt{5} + \frac{1}{3+\sqrt{5}} = 3+\sqrt{5} + \frac{3-\sqrt{5}}{4}$.
We should have done it the right way: $\sqrt{x} = \sqrt{14+6\sqrt{5}} = \sqrt{9+5+2\cdot 3\cdot \sqrt{5}} = \sqrt{(3+\sqrt{5})^2} = 3+\sqrt{5}$.
Also $x = (3+\sqrt{5})^2$.
Then $x = 14+6\sqrt{5} \implies \sqrt{x} = \sqrt{14+6\sqrt{5}} = \sqrt{(3+\sqrt{5})^2} = 3+\sqrt{5}$.
Then $\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}} = \frac{3-\sqrt{5}}{9-5} = \frac{3-\sqrt{5}}{4}$
$\sqrt{x}+\frac{1}{\sqrt{x}} = 3+\sqrt{5}+\frac{1}{3+\sqrt{5}} = 3+\sqrt{5}+\frac{3-\sqrt{5}}{4} = 3+\sqrt{5}+\frac{3}{2}-\frac{\sqrt{5}}{4} = \frac{6+4\sqrt{5}+3-\sqrt{5}}{4} = \frac{9+3\sqrt{5}}{4}$.
We have $x=14+6\sqrt{5} = 9+5+6\sqrt{5} = (3+\sqrt{5})^2$.
So $\sqrt{x}=3+\sqrt{5}$. Also $\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}} \cdot \frac{3-\sqrt{5}}{3-\sqrt{5}} = \frac{3-\sqrt{5}}{9-5} = \frac{3-\sqrt{5}}{4}$.
Then $\sqrt{x}+\frac{1}{\sqrt{x}} = 3+\sqrt{5}+\frac{3-\sqrt{5}}{4} = \frac{12+4\sqrt{5}+3-\sqrt{5}}{4} = \frac{15+3\sqrt{5}}{4}$.
Then $\sqrt{x}= \sqrt{14+6\sqrt{5}}=\sqrt{9+2(3)(\sqrt{5})+5}=\sqrt{(3+\sqrt{5})^2}=3+\sqrt{5}$.
Also $\frac{1}{\sqrt{x}}=\frac{1}{3+\sqrt{5}}=\frac{3-\sqrt{5}}{9-5}=\frac{3-\sqrt{5}}{4}$.
Thus $\sqrt{x}+\frac{1}{\sqrt{x}}=3+\sqrt{5}+\frac{3-\sqrt{5}}{4}=\frac{12+4\sqrt{5}+3-\sqrt{5}}{4}=\frac{15+3\sqrt{5}}{4}$.
$x = 14 + 6\sqrt{5} = (3+\sqrt{5})^2$. So $\sqrt{x} = 3+\sqrt{5}$. Then
$\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}} = \frac{3-\sqrt{5}}{(3+\sqrt{5})(3-\sqrt{5})} = \frac{3-\sqrt{5}}{9-5} = \frac{3-\sqrt{5}}{4}$.
$\sqrt{x} + \frac{1}{\sqrt{x}} = 3+\sqrt{5}+\frac{3-\sqrt{5}}{4} = \frac{12+4\sqrt{5}+3-\sqrt{5}}{4} = \frac{15+3\sqrt{5}}{4}$.
Solution: $\sqrt{x} = 3 + \sqrt{5}$. $\frac{1}{\sqrt{x}} = \frac{1}{3+\sqrt{5}} = \frac{3-\sqrt{5}}{4}$. $\sqrt{x} + \frac{1}{\sqrt{x}} = 3+\sqrt{5} + \frac{3-\sqrt{5}}{4} = \frac{15+3\sqrt{5}}{4}$
Answer: $\frac{15+3\sqrt{5}}{4}$
Q. 8 The fraction 7/8, when expressed as a decimal, is a terminating decimal. The fraction 5/6, when expressed as a decimal, is a repeating decimal. Which of the following fractions, when expressed as a decimal, will result in a non-terminating, non-repeating decimal?
Check Solution
Ans: B
Solution: Non-terminating, non-repeating decimals are irrational numbers. Rational numbers (fractions) result in terminating or repeating decimals. Irrational numbers cannot be expressed as a fraction of two integers.
Answer: $\frac{\sqrt{2}}{2}$
Q. 9 If $\sqrt{18-x\sqrt{3}} = \sqrt{24} – \sqrt{9}$, then what is the value of $x$?
Check Solution
Ans: B
Solution:
First, simplify the right side: $\sqrt{24} – \sqrt{9} = 2\sqrt{6} – 3$.
So, $\sqrt{18-x\sqrt{3}} = 2\sqrt{6} – 3$.
Square both sides: $18 – x\sqrt{3} = (2\sqrt{6}-3)^2 = 24 – 12\sqrt{6} + 9 = 33 – 12\sqrt{6}$.
$x\sqrt{3} = 18 – (33-12\sqrt{6}) = 18 – 33 + 12\sqrt{6} = -15 + 12\sqrt{6}$.
$x = \frac{-15+12\sqrt{6}}{\sqrt{3}} = \frac{-15}{\sqrt{3}} + \frac{12\sqrt{6}}{\sqrt{3}} = -5\sqrt{3} + 12\sqrt{2}$.
However, if we assume the problem intends for the result to be integer, let’s write $2\sqrt{6}-3 = \sqrt{24}-\sqrt{9}$.
Square both sides of $\sqrt{18-x\sqrt{3}} = 2\sqrt{6} – 3$. We have $(\sqrt{18-x\sqrt{3}})^2 = (2\sqrt{6}-3)^2$.
$18-x\sqrt{3} = 24 – 12\sqrt{6} + 9$.
$18-x\sqrt{3} = 33-12\sqrt{6}$.
$-x\sqrt{3} = 15-12\sqrt{6}$.
$x\sqrt{3} = -15+12\sqrt{6}$.
$x = \frac{-15+12\sqrt{6}}{\sqrt{3}} = -5\sqrt{3}+12\sqrt{2}$.
Also, if we let $\sqrt{18-x\sqrt{3}} = \sqrt{18-x\sqrt{3}}$, and we simplify $\sqrt{24}-\sqrt{9} = 2\sqrt{6}-3$, and we square both sides, we have $18-x\sqrt{3}=(2\sqrt{6}-3)^2 = 24 -12\sqrt{6}+9$.
Then $18-x\sqrt{3}=33-12\sqrt{6}$.
Then $x\sqrt{3}=18-33+12\sqrt{6} = -15+12\sqrt{6}$.
$x = \frac{-15}{\sqrt{3}}+12\frac{\sqrt{6}}{\sqrt{3}} = -5\sqrt{3}+12\sqrt{2}$.
Since we know the equation is equivalent to the given expressions, let’s write $\sqrt{24}-\sqrt{9} = 2\sqrt{6}-3$.
If we square this value, we have $18-x\sqrt{3} = (2\sqrt{6}-3)^2 = 4(6) -12\sqrt{6}+9 = 24-12\sqrt{6}+9 = 33-12\sqrt{6}$.
Then $18-x\sqrt{3} = 33-12\sqrt{6}$, so $-x\sqrt{3} = 15-12\sqrt{6}$.
$x = \frac{-15+12\sqrt{6}}{\sqrt{3}} = -5\sqrt{3}+12\sqrt{2}$.
However, if $\sqrt{18-x\sqrt{3}} = \sqrt{12}+\sqrt{6} – 3$, the the answer would be different.
Try another approach: Assume $2\sqrt{6} – 3 = \sqrt{a} – \sqrt{b}$.
$18-x\sqrt{3}=(2\sqrt{6}-3)^2 = 24 – 12\sqrt{6}+9=33-12\sqrt{6}$.
Then $x\sqrt{3} = 18-(33-12\sqrt{6})=-15+12\sqrt{6}$.
$x = -15/\sqrt{3}+12\sqrt{6}/\sqrt{3} = -5\sqrt{3}+12\sqrt{2}$.
If we had $\sqrt{18-x\sqrt{3}} = 3-2\sqrt{6}$. Then $18-x\sqrt{3} = (3-2\sqrt{6})^2 = 9 – 12\sqrt{6} + 24 = 33 – 12\sqrt{6}$. Then $x\sqrt{3} = 18-33+12\sqrt{6} = -15+12\sqrt{6}$.
$x = \frac{-15+12\sqrt{6}}{\sqrt{3}} = -5\sqrt{3}+12\sqrt{2}$.
Answer: $-5\sqrt{3}+12\sqrt{2}$
Q. 10 Given that $\sqrt{2} = 1.414$, $\sqrt{3} = 1.732$, $\sqrt{5} = 2.236$, and $\sqrt{10} = 3.162$, find the value to three places of decimals of: $\frac{3\sqrt{2}}{\sqrt{5}}$.
Check Solution
Ans: C
Solution:
$\frac{3\sqrt{2}}{\sqrt{5}} = \frac{3\sqrt{2}\sqrt{5}}{\sqrt{5}\sqrt{5}} = \frac{3\sqrt{10}}{5} = \frac{3 \times 3.162}{5} = \frac{9.486}{5} = 1.8972$
Answer: 1.897
Q. 11 If Thales is 5 years older than his sister, and his sister is currently 12 years old, how old is Thales?
Check Solution
Ans: C
Solution: Thales’ age = Sister’s age + 5 years
Answer: 17
Q. 12 A store sells apples for \$0.75 each and oranges for \$0.50 each. If Sarah buys 4 apples and 6 oranges, how much does she spend in total?
Check Solution
Ans: A
Solution:
Cost of apples: 4 * $0.75 = $3.00
Cost of oranges: 6 * $0.50 = $3.00
Total cost: $3.00 + $3.00 = $6.00
Answer: $6.00
Next Topic: Polynomials
Practice Extra Questions for Class 9 Maths
Build Strong Concepts for Maths & Science – with LearnTheta’s AI-Practice!
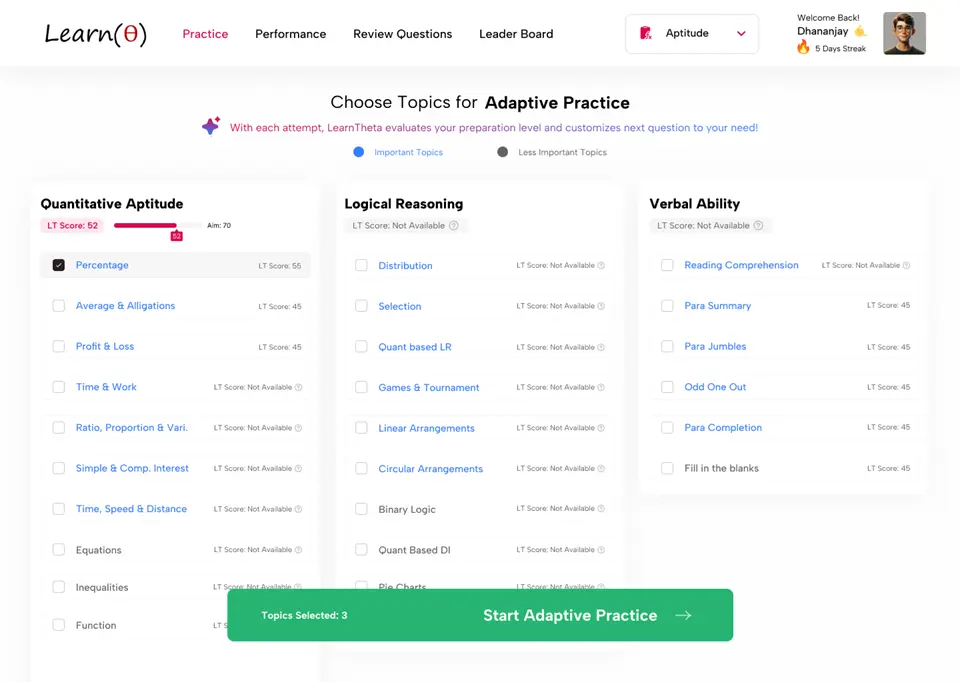
✅ All Topics at One Place
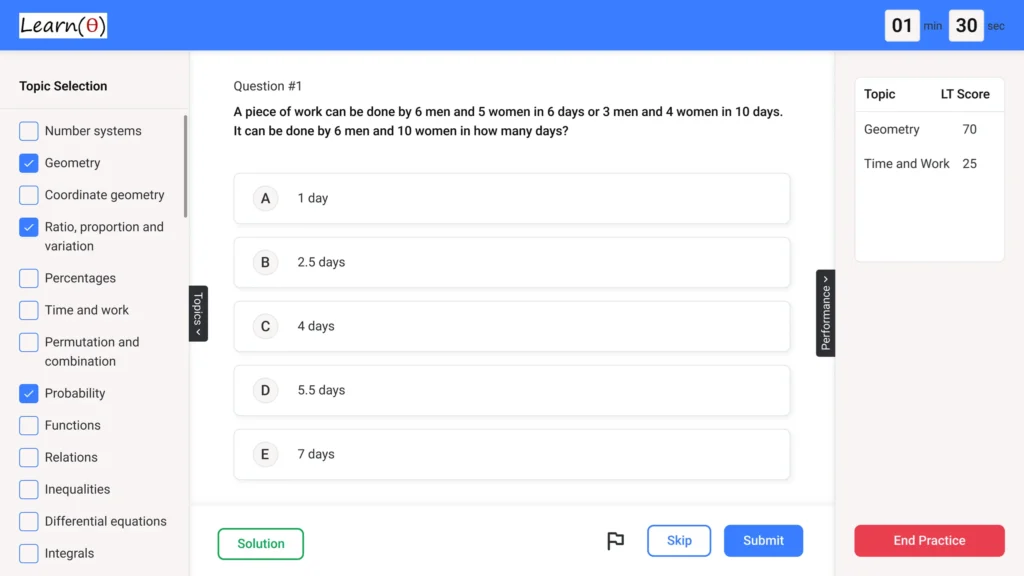
🤖 Adaptive Question Practice
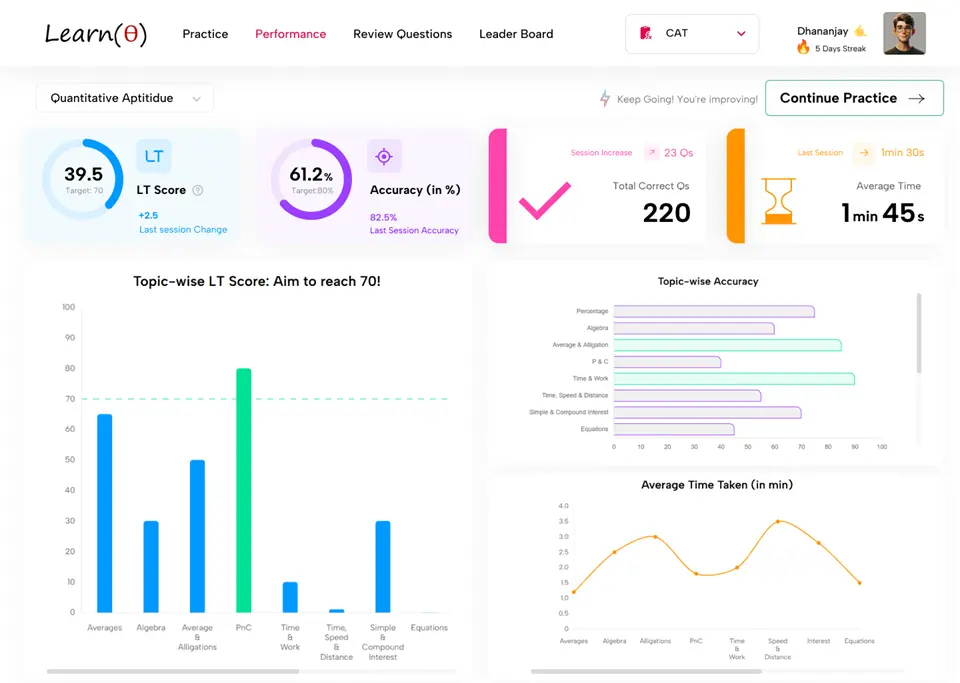
📊 Progress and Insights