CAT Quant: Statistics – Important Formulas and Concepts

Introduction

Statistics deals with collection, classification, presentation, analysis and interpretation of numeric data (quantitative data).
The quantitative data occurs in three forms namely
- Individual series
- Discrete series
- Continuous series.

A measure of central tendency indicates the central value of the size of a typical member of the group
Various measures discussed under central tendency are –
- Arithmetic Mean
- Geometric Mean,
- Harmonic Mean
- Median
- Mode

Given x₁, x₂, x₃, ….. x_n (n individual items), then – $$AM= \overline{x} = {\LARGE [} \ \frac{x_{1}+x_{2}+x_{3}…+x_{n}}{n} \ {\LARGE ]} \\ \overline{x} = \frac{Sum \ of \ the \ observations}{The \ number \ of \ observations}$$
For Example : The arithmetic mean of (4, 7, 8, 14, -13) is – $ \frac{4+7+8+14+(-13)}{5}=\frac{20}{5}=4 $
The algebraic sum of deviations about the mean is 0 or $ \Sigma(x-\overline{X})=0 $
The arithmetic mean to two numbers a, b is $ \frac{a+b}{2} $
For an AP series, AM is the arithmetic mean of equidistant terms.
If b = AM of (a,c) then a, b and c are in arithmetic progression.

Given x₁, x₂, x₃, ….. x_n (n individual items all being positive), then $$GM=\sqrt[n]{(x_{1}*x_{2} *…….*x_{n})} \\ GM = n_{th} \ root \ of \ the \ product \ of \ the \ numbers$$
For Example – The geometric mean of (50, 100, 200) is $ \sqrt[3]{(50\times100\times200)} = \sqrt[3]{(1000000)} = 100 $
The geometric mean of two positive numbers a, b is $ \sqrt{ab} $
If b=GM of (a,c), then a, b and c are in geometric progression.

Given x₁, x₂, x₃, ….. x_n (n individual observations such that none of them is equal to 0), then $$HM=\frac{n}{\frac{1}{x_{1}}+\frac{1}{x_{2}} + \frac{1}{x_{3}} +………….+\frac{1}{x_{n}}} $$
For Example : The harmonic mean of (2, 4, 6, 8, 10) is $ \frac{5}{\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{8}+\frac{1}{10}} = \frac{5 \times 120}{60+30+20+15+12} =\frac{600}{137} $
HM of two numbers a, b is \frac{2ab}{a+b}
If b=HM of (a,c), then a, b and c are in harmoni progression.

NOTE : For any two positive numbers a, b $$ AM \ge GM \ge HM \\ (GM) = \sqrt{ (AM) \times (HM)}$$

The median is the middle value of a dataset when it is arranged in ascending or descending order.
If the dataset has an odd number of values, the median is the middle value. For Example : The median of (five values) $ 4, 7, 12, 15, 20 \ \ is \ \ 12$ .
If the dataset has an even number of values, the median is the average of the two middle values. For Example : The median of $ 3, 5, 9, 11, 13,15 \ \ is \ \frac{9+11}{2}=10$
The median divides the distribution into two equal parts.
Median is suitable for qualitative data as well.

The is the item which is most often found in the given set of observations, Le, the value occurring the highest number of times.
A dataset can have one mode (unimodal), more than one mode (multimodal), or no mode if all values are unique.
For the observations – 2, 1, 1, 2, 3, 4, 3, 2, 1, 2, 2, 1, 4,6,7 : Mode = 2
For the observations – 5, 7, 11, 25, 36, 16. Here no item occurs more than once. So, mode is Ill-defined.

$ Mode = 3Median \ – \ 2Mean $
This formula is valid for the distribution which are moderately symmetric. (symmetry being coincidence of mean, median arid mode)

A measure of dispersion indicates the extent to which the different items of the group are spread about the average.
Various measures discussed under dispersion are –
- Range
- Quartile Deviation
- Mean Deviation
- Standard Deviation/Variance.

Given x₁, x₂, x₃, ….. x_n (n individual observations) $$ Range = [ \ maximum \ value \ – \ minimum \ value \ ]$$
For Example : Range of $ [7,4,8,1,6,11,15] = (15-1) = \ 14 $

Quartiles are those values, which divide the distribution into four equal parts, when the values are arranged in ascending or descending order of magnitude. $ \\ $
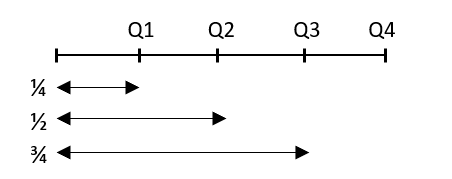
Q1 called the first quartile, Q2 is the middle quartile and Q3 the third quartile. The second quartile is also referred to as the median.
As the name semi-inter-quartile range itself suggests $$ QD =\frac{Q_{3}-Q_{1}}{2} \ [one-half \ the \ range \ of \ quartiles]$$
For calculation –
- Q₁ = size of $ {\LARGE(} \frac{n+1}{4}{\LARGE)}^{th} \ term $
- Q₃= size of $ 3{\LARGE(} \frac{n+1}{4}{\LARGE)}^{th} \ term $
- Note : The data is not in the ascending order (or in the descending order). So we arrange it first and then proceed.
For Example : Find the QD of the observations 5, 9, 13, 15, 21, 23 and 25 $ \\ Q_1 = {\LARGE(} \frac{7+1}{4}{\LARGE)}^{th} \ term = 2^{nd} \ term = 9 \\ Q_3 = 3{\LARGE(} \frac{7+1}{4}{\LARGE)}^{th} \ term = 6^{th} \ term = 23 \\ thus, \ QD = \frac{Q_{3}-Q_{1}}{2} = \frac{23-9}{2} = 7$

The mean deviation is calculated about mean or median or mode. But by default mean deviation is about mean.
Mean deviation is the average of deviations of each item in the data set from the mean. $$MD=\frac{\sum_{i=1}^{m}|x_{i}-A|}{n} \\ A = mean / median / mode \ ; \ n = number \ of \ items$$
For Examples : Find the mean deviation of 2, 5, 9, 11, 13 – $ \\ Mean \ of \ the \ observations \ \overline{x} = \frac{40}{5} = 8 \\ thus \ , \ MD = \frac{|2-8|+|5-8|+|9-8|+|11-8|+|13-8|}{5} =\frac{6+3+1+3+5}{5}=\frac{18}{5}=3.6 $
Mean Deviation of two numbers a, b = $ \frac{|a-b|}{2}$
Mean deviation is based on each and every observation.

Standard quantifies the amount of variation or dispersion from the average (mean) of the dataset.
A low standard deviation indicates that the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range of values.
Standard Deviation is the root mean squared deviation taken about the mean. $$SD= \sqrt{\frac{\Sigma(x_{i} – \overline{x})^{2}}{n}}, \ where x_1, x_2, x_3, ….. x_n \ are \ the \ items \ given. \\ The \ expression \ \sqrt{\frac{\Sigma(x_{i} – \overline{x})^{2}}{n}} \ also \ equals \ to \ \sqrt{\frac{\Sigma{x_{i}}^{2}}{n}-(\overline{x})^{2}} $$
For Example : Find the standard deviation of (2, 5, 7, 10, 13, 17) – $ Mean \ of \ the \ observations\ \overline{x} \ = \frac{54}{69} = 8 \\ thus, \ SD = \sqrt{\frac{\sum(x_{i}-\overline{x})^{2}}{n}} =\sqrt{\frac{(-7)^{2}+(-4)^{2}+(-2)^{2}+(1)^{2}+(4)^{2}+(8)^{2}}{6}} =\sqrt{\frac{49+16+4+1+16+64}{6}}=\sqrt{\frac{150}{6}} =\sqrt{25}=5 $
The square of the standard deviation is variance.
The standard deviation is always non-negative.