CAT Quant: Geometry – Important Formulas and Concepts
Basics
- Line – A straight path that extends infinitely in both directions and has no end points.
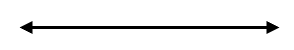
- Line Segment – A line segment is a part of a line that is bounded by two distinct endpoints. and has a finite length.

- Ray – A ray is a portion of a line that starts at a specific point (called the endpoint) and extends infinitely in one direction.
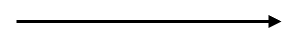
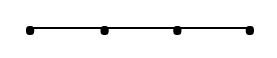
- Collinear Points – Three or more points are said to be collinear if they lie on the same line.
- Concurrent Lines – When all lines intersect at a single point, they are called concurrent lines.
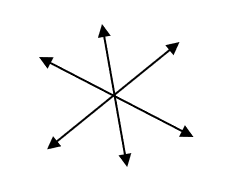
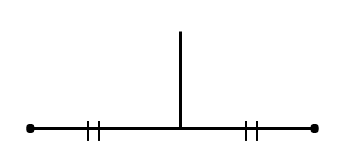
- Bisector – A line passing through the mid point of a line segment, it is said to be a Bisector of line segment.
Angles
- An angle is formed by two rays or line segments that share a common endpoint, known as the vertex of the angle. Denoted as \( \angle ABC \)where the middle term denotes the vertex.
- Angles are typically measured in degrees or radians.
- The sum of all angles made on one side of a straight line AB at a point O is \( 180^\circ \). One full rotation around a point is equivalent to \( 360^\circ \).
- Perpendicular – Two lines which makes an angle of \( 90^\circ \) with each other are said to be Perpendicular to each other.
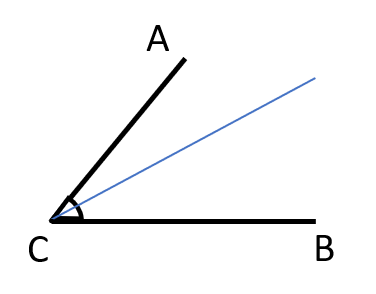
- Angle Bisector – A line passing through the vertex of an angle dividing the angle into two equal parts, the line is said to be an Angle Bisector. Any point on the angle bisector is equidistant from from the two arms of the angle.
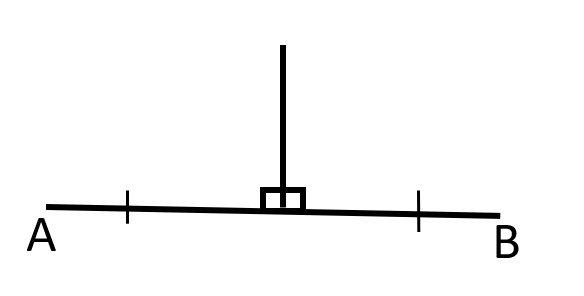
- Perpendicular Bisector – If a line is perpendicular to a line segment and passes through the midpoint of the line, it is said to be a Perpendicular Bisector. Any point on the perpendicular bisector is equidistant from the two end points of the segment.
- When two straight lines intersect each other, Vertically Opposite Angles are equal.
- Types of Angles –
- Acute Angle \( \longrightarrow \theta < 90^{\circ} \)
- Right Angle \( \longrightarrow \theta = 90^{\circ} \)
- Obtuse Angle \( \longrightarrow 90^{\circ} < \theta < 180^{\circ} \)
- Straight Angle \( \longrightarrow \theta = 180^{\circ} \)
- Reflex Angle \( \longrightarrow 180^{\circ} < \theta < 360^{\circ} \)
- Complementary Angles – Two angles whose sum is \( 90^{\circ} \) are Complementary Angles [\( \angle A + \angle B = 90^{\circ} \)].
- Supplementary Angles –Two angles whose sum is \( 180^{\circ} \) are Complementary Angles [\( \angle A + \angle B = 180^{\circ} \)].
Parallel Lines
- Two lines which are equidistant apart and do not have a common point are called Parallel lines.
- Transversal – When a straight line intersects two or more parallel lines at distinct points, then the cutting line is called the Transversal.
- If three or more parallel lines make intercepts on a transversal in a certain proportion , they make intercepts in the same proportion on any other transversal as well.
- When a straight line XY cuts two parallel lines PQ and RS as shown in the given figure the following relations hold – \( \\
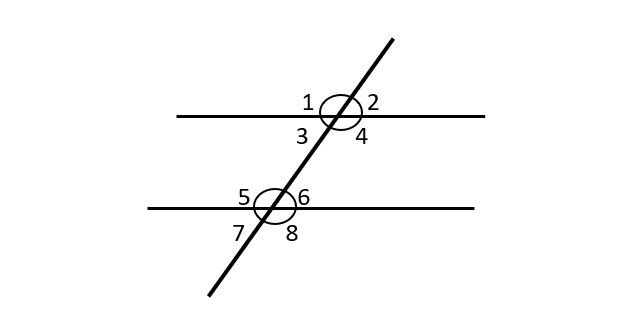
- Alternate Angles are \( \longrightarrow \) Equal \( \\ \angle 3 = \angle 6 \ ; \ \angle 4 = \angle 5 \)
- Opposite Angles are \( \longrightarrow \) Equal \( \\ \angle 1 = \angle 4 \ ; \ \angle 2 = \angle 3 \\ \angle 5 = \angle 8 \ ; \ \angle 6 = \angle 7 \)
- Corresponding Angles are \( \longrightarrow \) Equal \( \\ \angle 1 = \angle 5 \ ; \ \angle 2 = \angle 6 \\ \angle 3 = \angle 7 \ ; \ \angle 4 = \angle 8 \)
- Sum of Co-Interior Angles equals \( \longrightarrow \) 180\( ^{\circ} \) \( \\ \angle 4 + \angle 6 = 180^{\circ}\ \\ \angle 3 + \angle 5 = 180^{\circ} \)
- Sum of Exterior Angles equals \( \longrightarrow \) 180\( ^{\circ} \) \( \\ \angle 1 + \angle 7 = 180^{\circ}\ \\ \angle 2 + \angle 8 = 180^{\circ} \)
Triangles
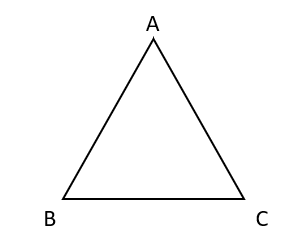
- A triangle is a polygon with three sides and three angles, formed by connecting three non-collinear points.
- The sum of the three angles of a triangle is 180°.
- The exterior angle of a triangle at each vertex is equal to the sum of the interior angles at the other two vertices. (Exterior angle is the angle formed at any vertex, by one side and the extended portion of the second side at that vertex).
- Altitude – The perpendicular drawn to a side with the opposite vertex is called the altitude of that side.
- Median – A line joining the midpoint of a side with the opposite vertex is called the median drawn to that side. A median divides the triangle into two equal halves as far as the area is concerned.
- If the sides are arranged in the ascending order of their length, then the angles opposite the sides (in the same order) will also be in ascending order (i.e., greater side has the greater angle opposite to it).
- There can be only one right angle or only one obtuse angle in any triangle. There can also not be one right angle and an obtuse angle both present in the same triangle.
Equilateral Triangle
- a triangle in which all sides and all angles are equal (each angle equal to 60\(^{\circ}\)) . \( \\ \)
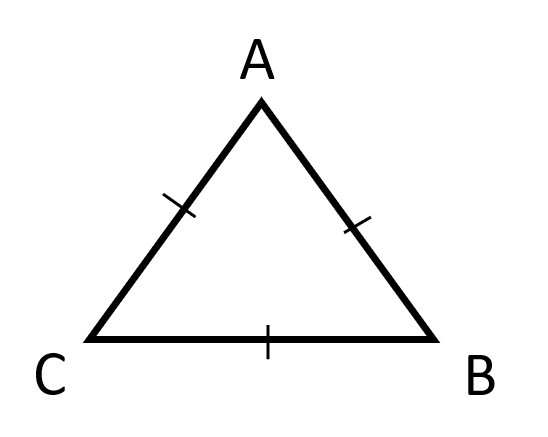
- In an equilateral triangle, the perpendicular bisector, the median and the altitude drawn to a particular side coincide and that will also be the angle bisector of the opposite angle.
- If a is the side of an equilateral triangle then its altitude is equal to \( \frac{\sqrt{3} a}{2} \).
- Sum of any two sides of a triangle is greater than the third side. Therefore, the difference of any two sides of a triangle is less than the third side. \( \\ \)

Isosceles Triangle
- A triangle in which two sides are equal is called an isosceles triangle and the angles opposite the equal sides are equal. \( \\ \)
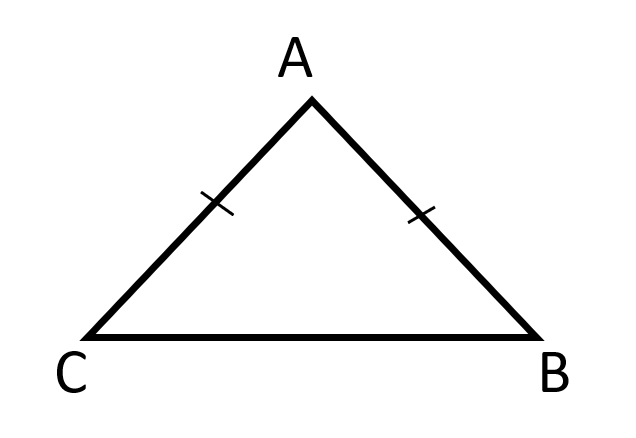
- In an isosceles triangle, the unequal side is called the BASE. The angle where the two equal sides meet is called the VERTICAL ANGLE.
- In an isosceles triangle, the perpendicular drawn to the base from the vertex opposite the base (i.e., the altitude drawn to the base) bisects the base as well as the vertical angle. That is, the altitude drawn to the base will also be the perpendicular bisector of the base as well as the angle bisector of the vertical angle. It will also be the median drawn to the base.
Scalene Triangle
- A scalene triangle is a type of triangle in which all three sides have different lengths, and hence no two angles are equal. \( \\ \)
- The perpendicular bisectors, medians, and altitudes of a scalene triangle intersect at different points compared to equilateral or isosceles triangles.
Right Angled Triangle
- A right-angled triangle is a type of triangle where one of the angles measures 90 degrees, called the right angle. \( \\ \)
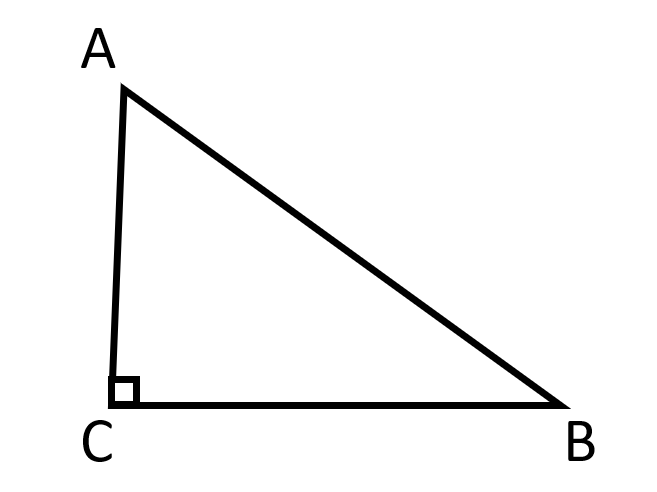
- In a right-angled triangle, the side opposite the right angle is called the hypotenuse (the longest side of a right angled triangle). The other two sides are called the base and height.
- Pythagoras Theorem – The fundamental property of a right-angled triangles is the Pythagorean theorem, which states that the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the legs (a and b). $$ c^2 = a^2 + b^2 $$
- Area – The area of a right-angled triangle can be calculated using the formula – $$ Area = \frac{1}{2} \times base \times height$$
- Pythagorean Triples – Pythagorean triplets are sets of three integers that form the sides of a right-angled triangle. When the lengths of the sides are integers, the triangle is called a Pythagorean triple. Pythagorean triplets can be further classified into primitive and non-primitive triplets.
- Primitive triplets have no common divisor greater than 1 between their elements
- Non-Primitive triplets can be obtained by scaling primitive triplets.
| PRIMITIVE TRIPLETS | NON-PRIMITIVE TRIPLETS |
| \( (3, 4, 5) \) | \( (6, 8, 10) \ , \ (9, 12, 15) \ , \ (12, 16, 20) \) |
| \( (5, 12, 13) \) | \( (10, 24, 26) \ , \ (15, 36, 39) \) |
| \( (8, 15, 17) \) | multiply the primitive triples with 2, 3, … and so on to form non-primitive triplets |
| \( (7, 24, 25) \) | multiply the primitive triples with 2, 3, … and so on to form non-primitive triplets |
| \( (9, 40, 41) \) | multiply the primitive triples with 2, 3, … and so on to form non-primitive triplets |
| \( 20, 21, 29) \) | multiply the primitive triples with 2, 3, … and so on to form non-primitive triplets |
Apollonius Theorem
- In a triangle ABC, if AD is the median from A to side BC (meeting BC at its mid point D), then \( \\ \)
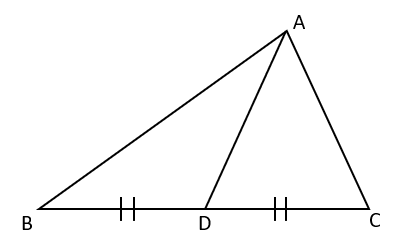 \( \\ AB^2 + AC^2 = 2(AD^2 + BD^2) \) This is called the Apollonius Theorem. This is useful in calculating the lengths of the three medians given the lengths of the three sides of the triangle.
\( \\ AB^2 + AC^2 = 2(AD^2 + BD^2) \) This is called the Apollonius Theorem. This is useful in calculating the lengths of the three medians given the lengths of the three sides of the triangle.
Angle Bisector Theorem
- In any triangle, the internal bisector of an angle bisects the opposite side in the ratio of the other two sides. In triangle ABC, if AD is the angle bisector of angle A, then \( \\ \)
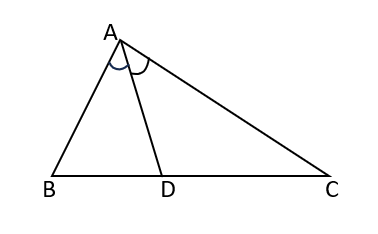 \( \\ {\large \frac{BD}{DC}= \frac{AB}{AC}} \\ Also , \ (BD \times AC) \ – \ (DC \times AB) = AD^2 \) This is called the Angle Bisector Theorem.
\( \\ {\large \frac{BD}{DC}= \frac{AB}{AC}} \\ Also , \ (BD \times AC) \ – \ (DC \times AB) = AD^2 \) This is called the Angle Bisector Theorem.
Geometric Centers of a Triangle
- Circumcenter –
- The three perpendicular bisectors of a triangle meet at a point called Circumcenter of the triangle. This is normally denotes as S. \( \\ \)
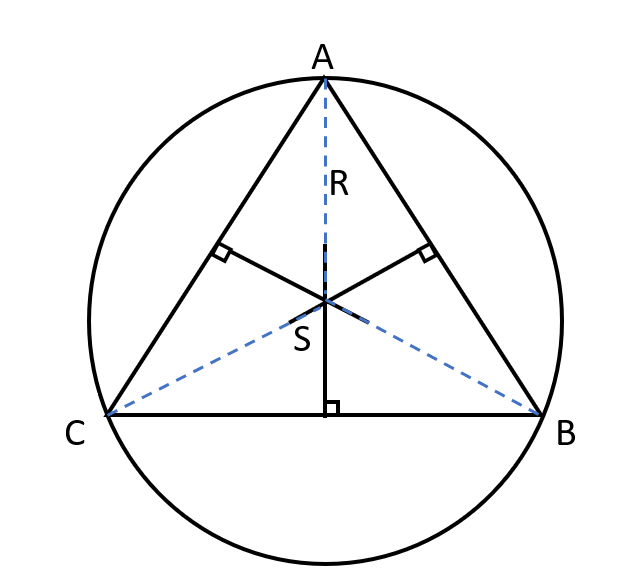
- The circumcenter of a triangle is equidistant from its vertices and the distance of circumcenter from each of the three vertices is called Circumradius (represented by R) of the triangle.
- The circle drawn with the circumcenter as center and circumradius as radius is called the Circumcircle of the triangle. It passes through all three vertices of the triangle.
- In a right angled triangle circumcircle – $$circumradius = \frac{hypotonus}{2} $$
- The three perpendicular bisectors of a triangle meet at a point called Circumcenter of the triangle. This is normally denotes as S. \( \\ \)
- Incentre and Excentres –
- The bisectors of the three angles of a triangle meet at a point called Incentre of the triangle. This is normally denoted as I. \( \\ \)
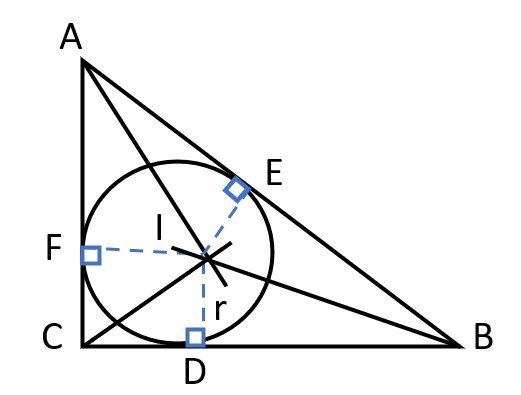
- The incentre is equidistant from the three sides of the triangle i.e., the perpendiculars drawn from the incentre to the three sides are equal in length and this length is called the Inradius (represented by r) of the triangle.
- The circle drawn with the incentre as center and the inradius as radius is called the Incircle of the triangle. It touches all three sides of the triangle.
- In the given figure, \( \\ \angle BIC = 90°+ \frac{1}{2} \angle A \) \( \\ \angle CIA = 90° + \frac{1}{2} \angle B \\ \angle AIB = 90° + \frac{1}{2} \angle C \)
- If the bisector of one angle and the bisectors of the external angles at the other two vertices are drawn, they meet at a point called Excentre. There are three excentres for any triangle – one corresponding to the bisector of each angle.
- The bisectors of the three angles of a triangle meet at a point called Incentre of the triangle. This is normally denoted as I. \( \\ \)
- Orthocenter –
- The three altitudes of a triangle meet at a point called Orthocenter. This is normally denoted as O. \( \\ \)
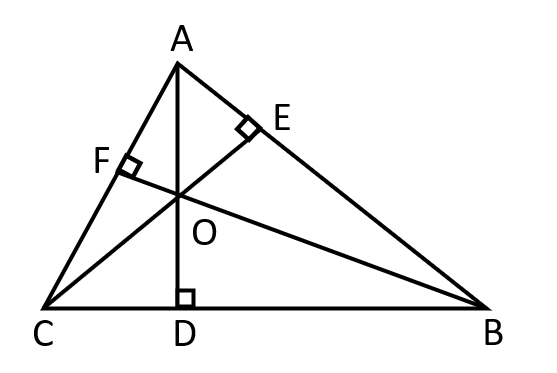
- In the given figure, \( \\ \angle BOC = 180°- \angle A \\ \angle COA = 180°- \angle B \\ \angle AOB = 180°- \angle C \)
- The three altitudes of a triangle meet at a point called Orthocenter. This is normally denoted as O. \( \\ \)
- Centroid –
- The three medians of a triangle meet at a point called the Centroid. This is normally denoted by G. \( \\ \)
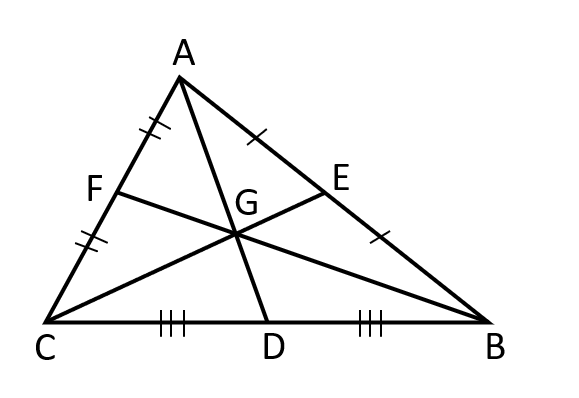
- The centroid divides each median into two segments, with the longer segment towards the vertex being twice as long as the shorter segment towards the midpoint of the opposite side.
- The three medians of a triangle meet at a point called the Centroid. This is normally denoted by G. \( \\ \)
Important points about geometric centers of a Triangle
- In an acute angled triangle, the circumcenter lies inside the triangle. In a right-angled triangle, the circumcenter lies on the hypotenuse of the triangle (it is the midpoint of the hypotenuse). In an obtuse angled triangle, the circumcenter lies outside the triangle.
- In an acute angled triangle, the orthocenter lies inside the triangle. In a right-angled triangle, the vertex where the right angle is formed (i.e., the vertex opposite the hypotenuse) is the orthocenter. In an obtuse angled triangle, the orthocenter lies outside the triangle.
- In a right-angled triangle the length of the median drawn to the hypotenuse is equal to half the hypotenuse. This median is also the circumradius of the right-angled triangle.
- The centroid divides each of the medians in the ratio 2:1, the part of the median towards the vertex being twice in length to the part towards the side.
- The inradius is less than half the smallest altitude of the triangle.
- In an isosceles triangle, the centroid, the orthocenter. the circumcenter and the incentre, all lie on the median to the base.
- In an equilateral triangle, the centroid, the orthocenter, the circumcenter and the incentre, all coincide.
- Hence, in equilateral triangle ABC
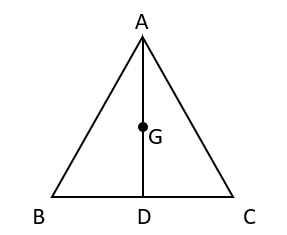 , AD is the median, altitude, angle bisector and perpendicular bisector. G is the centroid which divides the median in the ratio of 2: 1. Hence, \( AG = \frac{2}{3} AD \) and \( GD = \frac{1}{3} AD \).
, AD is the median, altitude, angle bisector and perpendicular bisector. G is the centroid which divides the median in the ratio of 2: 1. Hence, \( AG = \frac{2}{3} AD \) and \( GD = \frac{1}{3} AD \). - But since AD is also the perpendicular bisector and angle bisector and since G is the circumcenter as well as the incentre, AG is the circumradius and GD is the inradius of the equilateral triangle ABC. Since AD is also the altitude, its length is equal to \( \frac{\sqrt{3} a}{2} \) where a is the side of the equilateral, triangle. Hence, the circumradius of the equilateral triangle, \( R= \frac{2}{3} \cdot \frac{\sqrt{3} a}{2} = \frac{a}{\sqrt{3}} \) and the inradius \( (r) = \frac{1}{\sqrt{3}} \).
- Since the radii of the circumcircle and the incircle of an equilateral triangle are in the ratio 2: 1, the areas of the circumcircle and the incircle of an equilateral triangle will be in the ratio of \( 4:1 \).
- When the three medians of a triangle (i.e., the medians to the three sides of a triangle from the corresponding opposite vertices) are drawn, the resulting six triangles are equal in area and hence the area of each of these triangles is equal to one-sixth \( {\LARGE(} \frac{1}{6} {\LARGE)} \) of the area of the original triangle.
- All medians divide a \( \triangle \) into 6 equal parts \( \longrightarrow \) Area of each \( \triangle \) =\( {\LARGE(} \frac{1}{6} {\LARGE)} \) of original \( \triangle \).
Similarity of Triangles
- Two triangles are said to be similar if the three angles of one triangle are equal to the three angles of the second triangle.
- Similar triangles are alike in shape.
- The corresponding angles of two similar triangles are equal but the corresponding sides are only proportional and not necessarily equal.
- By “corresponding sides”, we mean that if we take a side opposite to a particular angle in one triangle, we should consider the side opposite to the equal angle in the second triangle.
- Similarity Rules – Two triangles are similar if –
- the three angles of one triangle are respectively equal to the three angles of the second triangle
- two sides of one triangle are proportional to two sides of the other
- the included angles are equal, or if the three sides of one triangle are proportional to the three sides of another triangle.
- In two similar triangles –
- Ratio of corresponding sides = Ratio of heights (altitudes) = Ratio of the lengths of the medians = Ratio of the lengths of the angle bisectors = Ratio of inradii = Ratio of circumradii = Ratio of perimeters.
- Ratio of areas = Ratio of squares of corresponding sides.
- Note – In a right-angled triangle, the altitude drawn to the hypotenuse divides the given triangle into two similar triangles, each of which is in turn similar to the original triangle.
Congruency of Triangles
- Two triangles will be congruent if at least one of the following conditions is satisfied –
- SSS Congruency – Three sides of one triangle are respectively equal to the three sides of the second triangle (normally referred to as the S-S-S rule, i.e., the side-side-side congruence).
- SAS Congruency – Two sides and the included angle of one triangle are respectively equal to two sides and the included angle of the second triangle (normally referred to as the S-A-S rule, i.e., side-angle-side congruence).
- ASA Congruency – Two angles and the included side of a triangle are respectively equal to two angles and the included side of the second triangle (normally referred to as the A-S-A rule, i.e., angle-side-angle congruence). (Note: Hence AAS is also a sufficient condition for congruence.)
- RHS Congruency – Two right-angled triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to hypotenuse and one side of the second triangle (normally referred to as the R-H-S rule, i.e., right-hypotenuses-side congruence).
- In two congruent triangles –
- the corresponding sides (i.e., sides opposite to corresponding angles) are equal.
- the corresponding angles (angles opposite to corresponding sides) are equal.
- the areas of the two triangles will be equal.
Important Points about Triangles
- Basic Proportionality Theorem – a line drawn parallel to one side of a triangle divides the other two sides in the same proportion.
- For example, in the given figure,
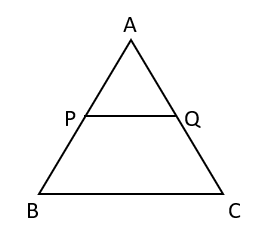 PQ is drawn parallel to BC in \( \triangle ABC \). This will divide the other two sides AB and AC in the same ratio, i.e., \( \frac{AP}{PB} = \frac{AQ}{QC} \).
PQ is drawn parallel to BC in \( \triangle ABC \). This will divide the other two sides AB and AC in the same ratio, i.e., \( \frac{AP}{PB} = \frac{AQ}{QC} \). - Conversely, a line joining two points lying on different sides of a triangle, dividing the respective sides in the same ratio, is parallel to the third side.
- If in the given figure, P divides AB in the ratio m: n and Q divides AC in the ratio m: n, the line joining P and Q is parallel to the third side BC.
- Also, the length of PQ = \( {\LARGE(} \frac{m}{m+n} {\LARGE)} BC \).
- For example, in the given figure,
- Mid Point Theorem – it states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. In the above given triangle, \( \triangle ABC \longrightarrow \ PQ = \frac{1}{2} \ BC \).
- Parallelogram Law of Area – two triangles having the same base and lying between the same pair of parallel lines have their areas equal. In the given figure,
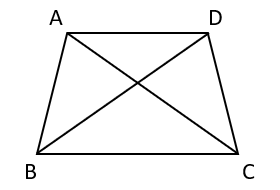 AD is parallel to BC. Hence, area of \( \triangle ABC \)= area of \( \triangle DBC \).
AD is parallel to BC. Hence, area of \( \triangle ABC \)= area of \( \triangle DBC \).
Quadrilaterals
- Any four-sided closed figure is called a quadrilateral. \( \\ \)
- By imposing certain conditions on the sides and/or angles of a quadrilateral, we can get the figures trapezium, parallelogram, rhombus, rectangle, square.
- The sum of the four angles of a quadrilateral is equal to 360°.
- Sum of 3 sides of a quadrilateral is greater than 4th side.
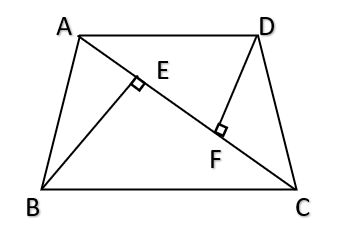
- The perpendiculars drawn to a diagonal (in a quadrilateral) from the opposite vertices are called “offsets”. In the above figure BE and DF are the offsets drawn to the diagonal AC.
- There are several types of quadrilaterals, each with its own unique set of properties and characteristics. Some of the most common types of quadrilaterals include trapezium, parallelogram, rhombus, rectangle and square.
- Cyclic Quadrilateral –
- If the four vertices of a quadrilateral lie on the circumference of a circle (i.e., if the quadrilateral can be inscribed in a circle) it is called a cyclic quadrilateral . In a cyclic quadrilateral, the sum of opposite angles = 180° i.e., in the given figure, \( A+C=180^{\circ} \) and \( B+D= 180^{\circ} \) \( \\ \).
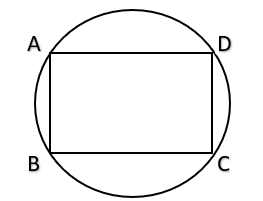
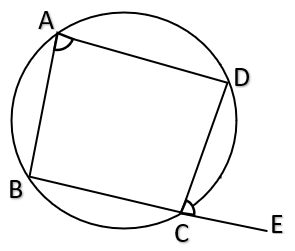
- Also, in a cyclic quadrilateral, any exterior angle is equal to the interior angle at the opposite vertex i.e., in the given figure, \( ∠DCE = ∠BAD \) \( \\ \)
- If the four vertices of a quadrilateral lie on the circumference of a circle (i.e., if the quadrilateral can be inscribed in a circle) it is called a cyclic quadrilateral . In a cyclic quadrilateral, the sum of opposite angles = 180° i.e., in the given figure, \( A+C=180^{\circ} \) and \( B+D= 180^{\circ} \) \( \\ \).
Trapezium
- If one side of a quadrilateral is parallel to the opposite side, then it is called a trapezium.
- The two sides other than the parallel sides in a trapezium are called the oblique sides.
- In the given figure, ABCD is a trapezium, in which AD is parallel to BC. \( \\ \)
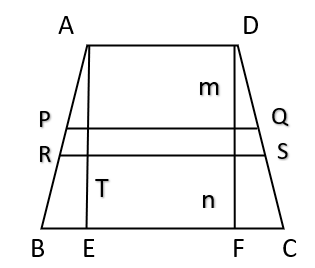
- If the midpoints of the two oblique sides are joined, it is equal in length to the average of the two parallel sides, i.e., in the above figure, \( PQ = \frac{1}{2}[AD +BC] \)
- In general, if a line is drawn in between the two parallel sides of the trapezium such that it is parallel to the parallel sides and also divides the distance between the two parallel sides in the ratio \( m:n \) (where the portion closer to the shorter of the two parallel sides is m), the length of the line is given by – $$\frac{m}{m+n} (Longer \ side) + \frac{n}{m+n}(Shorter side)$$ where shorter side and longer side refer to the shorter and longer of the two parallel sides of the trapezium.
- In the given figure, RS is the line parallel to AD and BC and the ratio of the distances DT and TE is m: n. The length of RS is given by \( \frac{m}{m+n} (BC) + \frac{n}{m+n}(AD) \)
Parallelogram
- A quadrilateral in which both pairs of opposite sides are parallel is called a parallelogram.
- In a parallelogram –
- both pairs of opposite sides are equal
- both pairs of opposite angles are equal
- Sum of any two adjacent angles is 180°.
- Each diagonal divides the parallelogram into two congruent triangles.
- The diagonals are equal and bisect each other. \( \\ \)
- If two adjacent angles of a parallelogram are equal, then all four angles will be equal and each in turn will be equal to 90°. Then the figure will be a rectangle.
- If any two adjacent sides of a parallelogram are equal, then all four sides are equal to each other and the figure is a rhombus.
- If there is a parallelogram and a triangle with the same base and between the same parallel lines, then the area of the triangle will be half that of the parallelogram.
- If there is a parallelogram and a rectangle with the same base and between the same parallel lines, then the areas of the parallelogram and the rectangle will be the same.
- The figure formed by joining the midpoints of the sides of any quadrilateral taken in order, is a parallelogram, and its area is half the area of the original triangle.
Rhombus
- A rhombus is a parallelogram in which all sides are equal. (Note: If in a parallelogram, one pair of adjacent sides are equal, it is a rhombus). \( \\ \)
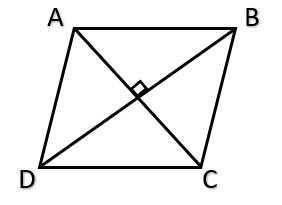
- Since a rhombus is a parallelogram, all the properties of a parallelogram apply to a rhombus.
- In a rhombus, the diagonals bisect each other perpendicularly. Conversely, any quadrilateral where the two diagonals bisect each other at right angles is a rhombus.
- The four triangles that are formed by the two bisecting diagonals with the four sides of the rhombus are all congruent.
- Side of a rhombus = \( \sqrt{\frac{1}{4} ( Sum \ of \ squares \ of \ the \ diagonals} ) \)
Rectangle
- A rectangle is also a special type of parallelogram and hence all properties of a parallelogram apply to rectangles also.
- A rectangle is a parallelogram in which two adjacent angles are equal. Therefore, each of the angles is equal to 90°. \( \\ \)

- The diagonals of a rectangle are equal and bisect each other.
- When a rectangle is inscribed in a circle, the diagonals become diameters of the circle.
- If a and b are the two adjacent sides of a rectangle, then the diagonal is given by \( \sqrt{a² + b²} \)
- If a rectangle and a triangle are on the same base and between the same parallels, then the area of the triangle will be equal to half the area of the rectangle.
Square
- A square is a rectangle in which all four sides are equal (or a rhombus in which all four angles are equal, i.e., all are right angles). \( \\ \0
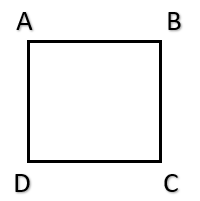
- The diagonals are equal and they bisect at right angles. So, all the properties of a rectangle as well as those of a rhombus hold good for a square.
- Diagonal = \( \sqrt{2} \times (Sides) \).
- When a square is inscribed in a circle, the diagonals become the diameters of the circle.
- When a circle is inscribed in a square, the side of the square is equal to the diameter of the circle.
- The largest rectangle that can be inscribed in a given circle will be a square.
Polygon
- Any closed figure with three or more sides is called a polygon.
- Types of Polygon – Polygons can majorly be divided into two types which are –
- Convex Polygon : \( \\ \)
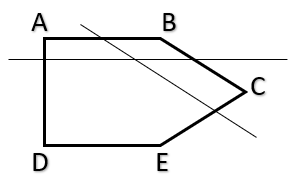
- In a convex polygon, all interior angles are less than 180 degrees.
- The line segment connecting any two points within the polygon lies entirely inside the polygon.
- No line segment joining two points on the boundary of the polygon passes outside the polygon.
- Examples of convex polygons include equilateral triangles, squares, regular pentagons, regular hexagons, and so on.
- Concave Polygon : \( \\ \)
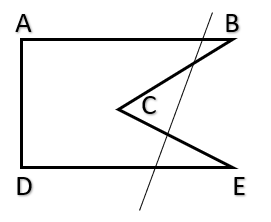
- In a concave polygon, at least one interior angle is greater than 180 degrees.
- A concave polygon has at least one “caved-in” or “indented” portion, where a line segment joining two points on the boundary of the polygon passes outside the polygon.
- Examples of concave polygons include regular octagons with one side removed, irregular hexagons with a deep inward angle, or irregular pentagons with one or more angles greater than 180 degrees.
- Convex Polygon : \( \\ \)
- Regular Polygon – A regular polygon is a convex polygon in which all sides are equal and all angles are equal. A regular polygon can be inscribed in a circle. The centre of the circumscribing circle (the circle in which the polygon is inscribed) of a regular polygon is called the centre of the polygon.
- The names of polygons with three, four, five, six, seven, eight, nine and ten sides are respectively triangle, quadrilateral, pentagon, hexagon, heptagon, octagon, nonagón and decagon.
- The sum of interior angles of a convex polygon $$ = (2n-4) 90^{\circ} \ or \ (n-2)180^{\circ} $$ where n is the number of the sides of the polygon.
- In a regular polygon of n sides, if each of the interior angles is \( d^\circ \), then $$d=\frac {2n-4}{n} (90^{\circ}) $$ and each exterior equals \( = \frac{360°}{n} \)
- If the center of a regular polygon (with n sides) is joined with each of the vertices, we get n identical triangles inside the polygon. In general, all these triangles are isosceles triangles. Only in case of a regular hexagon, all these triangles are equilateral triangles, i.e., in a regular hexagon, the radius of the circumscribing circle (r) is equal to the side of the hexagon (a), thus r = a.
- A line joining any two non-adjacent vertices of a polygon is called a diagonal. A polygon with n sides will have \( \frac{n(n-3)}{2} diagonals \)
Circles
- A circle is a closed curve drawn such that any point on the curve is equidistant from a fixed point.
- Centre and Radius – The fixed point is called the center of the circle and the distance from the center to any point on the circle is called the radius of the circle.
- Diameter – A diameter of a circle is a straight line passing through the center of the circle and joining two points on the circle. A circle is symmetric about any diameter. \( \\ \)
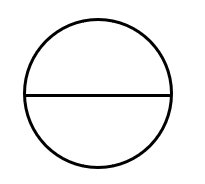
- Chord – A chord is a point joining any two points on the circumference of a circle. A diameter is the longest chord in a circle. \( \\ \)
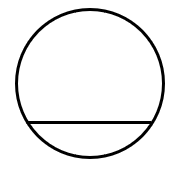
- Secant – A secant is a line intersecting a circle in two distinct points and extending outside the circle also. \( \\ \)
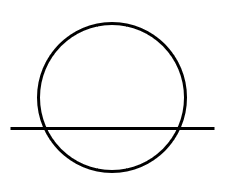
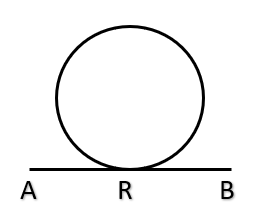
- Tangent – A line that touches the circle at only one point is a tangent to the circle (AB is a tangent touching the circle at the point R in the given figure ). \( \\ \)
Important Points about Circles
- If PAB and PCD are two secants then \( PA \cdot PB = PC \cdot PD \). \( \\ \)
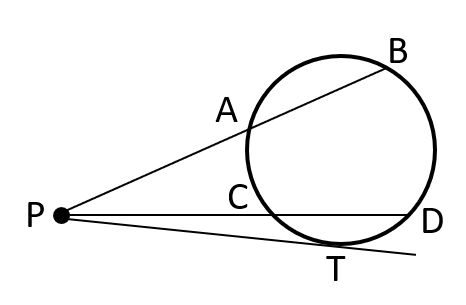
- If PAB and PCD are secants and PT is a tangent to the circle at T , then \( PA \cdot PB = PC \cdot PD = (PT)^2 \) .
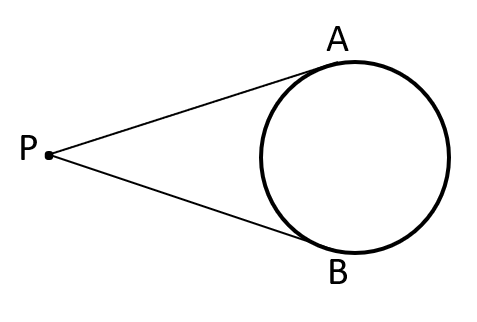
- Two tangents can be drawn to the circle from any point outside the circle and these two tangents are equal in length. In the given figure, P is the external point and the two tangents PA and PB are equal. \( \\ \)
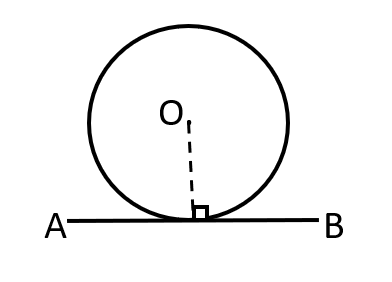
- A tangent is perpendicular to the radius drawn at the point of tangency . Conversely, if a perpendicular is drawn to the tangent at the point of tangency, it passes through the center of the circle. \( \\ \)
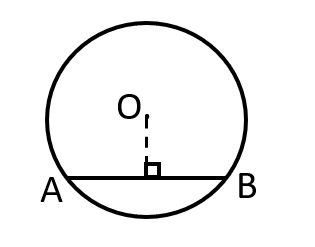
- A perpendicular drawn from the center of the circle to a chord bisects the chord (In the given figure, the perpendicular from O to the chord AB bisects AB) and conversely, the perpendicular bisector of a chord passes through the center of the circle. \( \\ \)
- Two chords that are equal in length will be equidistant from the center, and conversely two chords which are equidistant from the center of the circle will be of the same length. Equal chords subtend equal angle at the center.
- Two circles are said to touch each other if a common tangent can be drawn touching both the circles at the same point. This is called the point of contact of the two circles. The two circles may touch each other internally or externally. When two circles touch each other, then the point of contact and the centers of the two circles are collinear, i.e., the point of contact lies on the line joining the centers of the two circles.
- If two circles touch internally, the distance between the centers of the two circles is equal to the difference in the radii of the two circles \( (R-r) \). When two circles touch each other externally, then the distance between the centers of the two circles is equal to the sum of the radii of the two circles \( (R+r) \).
- Types of Tangent –
- A line which is tangent to two circles is called a common tangent.
- In general, for two circles, there can be anywhere from zero to four common tangents drawn depending on the position of one circle in relation to the other.
- Direct Common Tangent :
- Tangent that directly touches both circles, without intersecting the line joining their centers.
- It touches the circles on the same side of the line connecting their centers.
- Direct common tangents can be external or internal.
- Length of Direct Common Tangent = \( \sqrt{d^2 – (R-r)^2} \) where, d = distance between centers. \( \\ \)
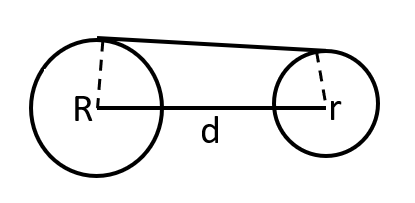
- Transverse Common Tangent :
- Tangent that intersects with the line joining the centers of the circles.
- It touches the circles on opposite sides of the line connecting their centers.
- Transverse common tangents can only be external.
- Length of Transverse Common Tangent = \( \sqrt{d^2 – (R+r)^2} \) where, d = distance between centers. \( \\ \)
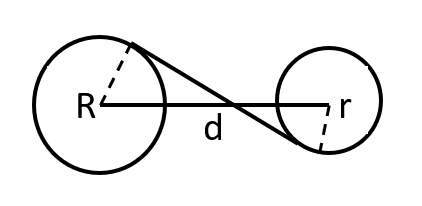
- Direct Common Tangent :
- Two circles are said to be concentric if they have the same center. For two concentric circles, the circle with the smaller radius lies completely within the circle with the bigger radius.
Arcs and Sectors
- Arc –
- An arc is a connected part of a circle. In the given figure, ACB is called minor arc and ADB is called major arc.
- In general, if we talk of an arc AB, we refer to the minor arc. AOB is called the angle formed by the arc AB (at the center of the circle).
- The angle subtended by an arc at the center is double the angle subtended by the arc at any point X (or Y) on the remaining part of the circle. \( \\ \)
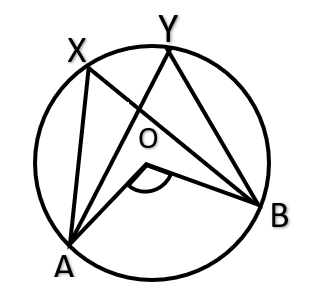
- In the given figure, \( \angle AOB = 2( \angle AXB) = 2( \angle AYB) \)
- Angles in the same segment are equal. In the above figure. \( \angle AXB = \angle AYB \)
- Alternate Segment Theorem –
- The angle between a tangent and a chord through the point of contact of the tangent is equal to the angle made by the chord in the alternate segment (i.e., segment of the circle on the side other than the side of location of the angle between the tangent and the chord). \( \\ \)
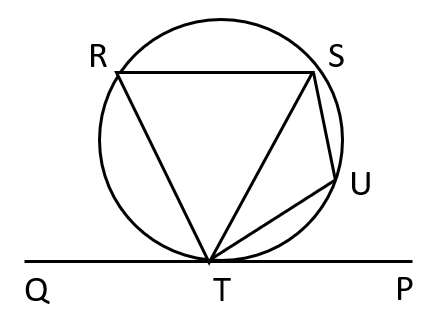
- In the given figure, PQ is a tangent to the circle at the point T and TS is a chord drawn at the point of contact. Considering PTS which is the angle between the tangent and the chord, the angle TRS is the angle in the “alternate segment”.
- \( \angle PTS = \angle TRS \ and \ \angle QTS = \angle TUS \)
- The angle between a tangent and a chord through the point of contact of the tangent is equal to the angle made by the chord in the alternate segment (i.e., segment of the circle on the side other than the side of location of the angle between the tangent and the chord). \( \\ \)
- Sector –
- The region bounded by an arc and the two radii at the two end points of the arc is called sector.
- In the given figure, the shaded figure AOB is called the minor sector. The rest of the circle is the major sector. \( \\ \)
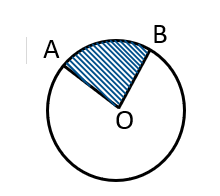
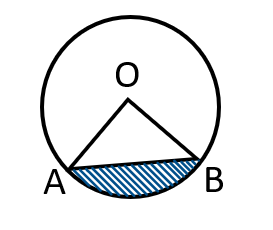
- Segment –
- The region bounded by an arc and the line segment joining the endpoints of the arc is called a segment of a circle (or circular region).
- In the given figure, the shaded region is a minor segment. The rest of the circular region is a major segment. \( \\ \)