Simplification Questions and Answers – Free Practice!
Refer Concepts for Simplification
Q. 1 Simplify: \( \frac{(45)^2 – (15)^2}{30} \)
Check Solution
Ans: A
Use the identity $ a^2 – b^2 = (a – b)(a + b) $, then divide: $ \frac{30 \times 60}{30} = 60 $
Q. 2 Simplify: \( \sqrt{2025} + \sqrt{1225} – \sqrt{625} \)
Check Solution
Ans: B
All the given expressions are standard squares. You are not supposed to rememebr squares beyond 30, but if you take out 25 from each fo the expression, it becomes obvious:
Roots: $ 5 (\sqrt{81} + \sqrt{49} – \sqrt{25}) = 55 $
Q. 3 Simplify the expression: \( \frac{2}{5} + \frac{3}{10} – \frac{4}{15} \)
Check Solution
Ans: D
LCM = 30 → $ \frac{12+9-8}{30} = \frac{13}{30} $
Q. 4 Simplify: \( \frac{1}{2} \div \left( \frac{3}{4} \times \frac{2}{3} \right) \)
Check Solution
Ans: C
$ \frac{3}{4} \times \frac{2}{3} = \frac{1}{2}, \frac{1}{2} \div \frac{1}{2} = 1 $
Q. 5 Simplify: \( (3.2)^2 – (1.2)^2 \)
Check Solution
Ans: B
$ a^2 – b^2 = (4.4)(2.0) = 8.8 $
Preapring for Banking, CAT, SSC or Placement?
Practice questions with LearnTheta. It adapts to your level, helping you prepare faster & smarter.
Q. 6 Simplify: \( \frac{(2 + \frac{1}{2})^2}{(1 + \frac{1}{4})} \)
Check Solution
Ans: A
$ (\frac{5}{2})^2 = \frac{25}{4}, \div \frac{5}{4} = 5 $
Q. 7 Simplify: \( \frac{3}{2} + \frac{4}{3} – \frac{5}{6} \)
Check Solution
Ans: A
Convert to common denominator → $ \frac{9 + 8 – 5}{6} = \frac{12}{6} = 2 $
Q. 8 Simplify: \( \left( \frac{5}{6} \right)^2 + \left( \frac{1}{2} \right)^2 \)
Check Solution
Ans: D
$ \frac{25}{36} + \frac{9}{36} = \frac{34}{36} = \frac{17}{18} $
Q. 9 Simplify: \( \sqrt{144} + \sqrt{121} – \sqrt{81} \)
Check Solution
Ans: C
$ \sqrt{144} = 12, \sqrt{121} = 11, \sqrt{81} = 9 → 12 + 11 – 9 = 14 $

Practice Simplification Questions – Smart Way!
Placement Tests | Bank Exams | SSC CGL
Q. 10 Simplify: \( \frac{1}{(1 – \frac{1}{2})} + \frac{1}{(1 – \frac{1}{3})} \)
Check Solution
Ans: B
$ \frac{1}{\frac{1}{2}} + \frac{1}{\frac{2}{3}} = 2 + \frac{3}{2} = \frac{7}{2} $
Q. 11 Simplify: $\sqrt{[\frac{2.4 × 2.4)}{(1.2 × 3.6)}]^2 + 1}$
Check Solution
Ans: C
Dividing the fractions by 1.2 will give $ \sqrt{(\frac{4}{3})^2 + 1} = \sqrt{(16+9)/9} = 5/3 $
Q. 12 Simplify: $\sqrt{98} + \sqrt{8}$
Check Solution
Ans: C
$\sqrt{98} + \sqrt{8} = 7\sqrt{2} + 2\sqrt{2} = 9\sqrt{2} = \sqrt{162}$
Q. 13 (48% of 850 + 35% of 960) ÷ (0.2 × 8)
Check Solution
Ans: D
48% of 850 = 408, 35% of 960 = 336, Sum = 744; Denominator = 1.6; 744 ÷ 1.6 = 465
Q. 14 √784 + (56 ÷ 7) × 9 – 15² ÷ 5
Check Solution
Ans: C
√784 = 28, (56÷7)×9 = 72, 15²÷5 = 45; 28 + 72 – 45 = 55
Q. 15 $125 × 8^{2/3} ÷ 5^3$
Check Solution
Ans: A
$8^(2/3) = 4; So (125×4) ÷ 125 = 4$
Q. 16 (42² – 28²) ÷ 14
Check Solution
Ans: A
Use a²−b²=(a−b)(a+b); (42−28)(42+28)/14 = 14×70/14 = 70
Q. 17 (18.75% of 640) + (125 ÷ 25) × 3²
Check Solution
Ans: C
18.75% = 3/16; (3/16)×640=120; (125÷25)×3²=45; Total=165
Next Topic Number System
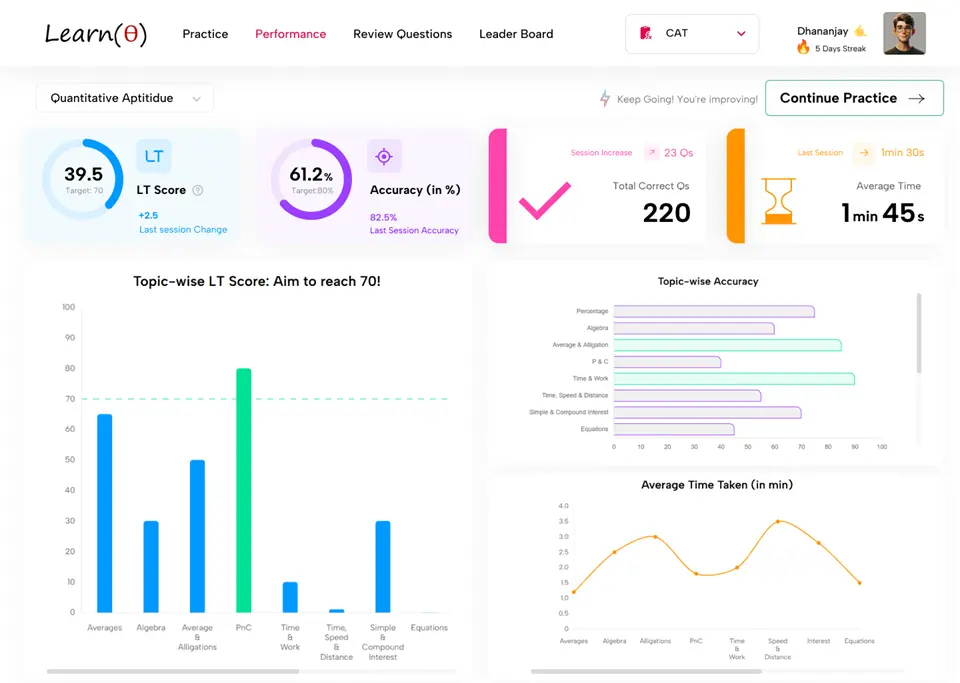
Refer Thousands of Quantitative Aptitude Questions with Answers and Detailed Solutions
Important Aptitude Qs for Comeptititve Exams
Aptitude Question Shorts
LearnTheta Adaptive Practice Demo
Crack Exams Fast & Smart with Adaptive Practice!
Placement | Banking | SSC CGL | CAT
✅ All Topics at One Place
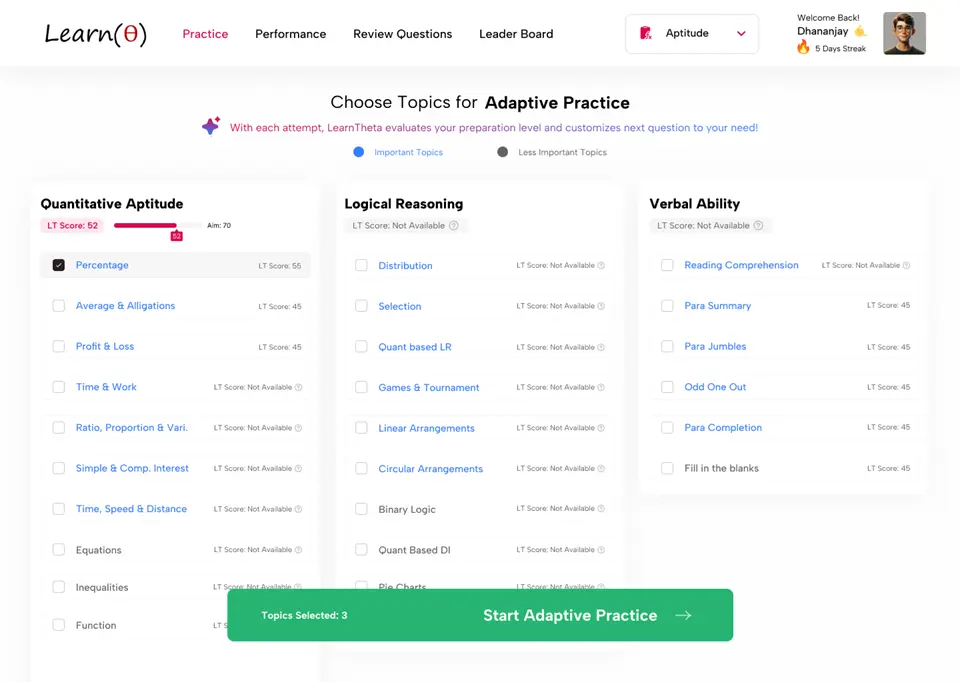
🤖 Adaptive Question Practice
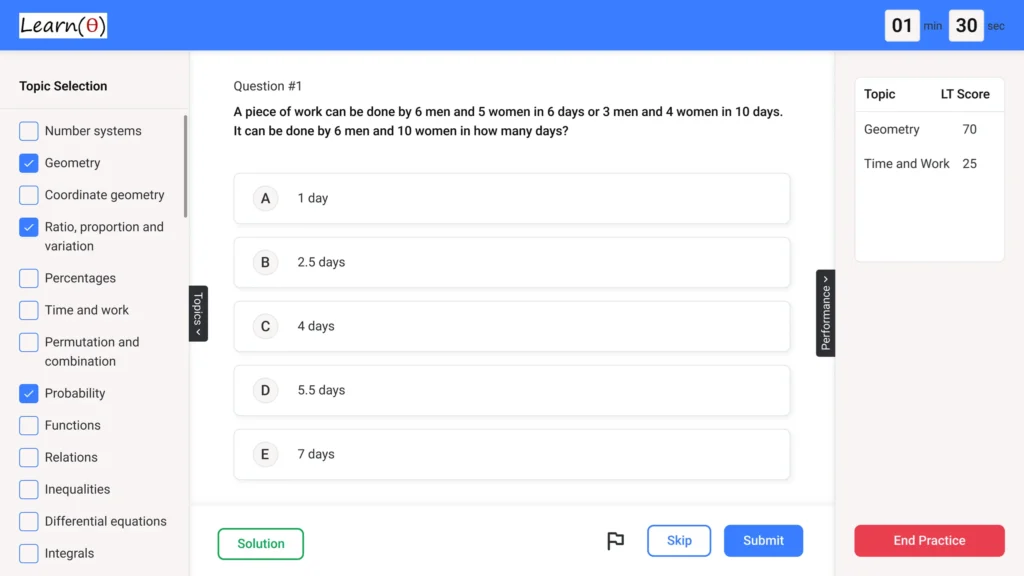
📊 Progress and Insights