Algebra: SSC CGL Practice Questions
Q. 1 Expand: (2x – y + 5z)²
Check Solution
Ans: A
Explanation: We can use the formula (a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ac, where a = 2x, b = -y, and c = 5z.
So, (2x – y + 5z)² = (2x)² + (-y)² + (5z)² + 2(2x)(-y) + 2(-y)(5z) + 2(2x)(5z)
= 4x² + y² + 25z² – 4xy – 10yz + 20xz
Q. 2 Find the term without any ‘x’ in the result when you expand the expression (5x² – 1/x)³.
Check Solution
Ans: B
Explanation: We need to find the term without any ‘x’ when expanding (5x² – 1/x)³. Using the binomial theorem, the general term is given by: T(r+1) = ₖCᵣ * (5x²)⁽ᵏ⁻ʳ⁾ * (-1/x)ʳ = ₖCᵣ * 5⁽ᵏ⁻ʳ⁾ * x²⁽ᵏ⁻ʳ⁾ * (-1)ʳ * x⁻ʳ, where k=3
Combining the powers of x, we have: x^(2(3-r) – r) = x^(6-2r-r) = x^(6-3r)
For the term without x, the power of x must be 0. So, we need to find r such that: 6-3r = 0.
Solving for r: 3r = 6, which gives r = 2.
Now, substituting r = 2 into the general term formula:
T(2+1) = T(3) = ₃C₂ * (5x²)⁽³⁻²⁾ * (-1/x)² = ₃C₂ * 5¹ * x² * 1/x² = 3 * 5 * 1 = 15.
So, the term without x is 15.
Correct Option: B
Q. 3 Given that x plus 16 divided by x equals 8, what is the value of x squared plus 32 divided by x squared?
Check Solution
Ans: B
Explanation: First, solve for x from the given equation x + 16/x = 8. Multiply both sides by x: x^2 + 16 = 8x. Rearrange the equation to get a quadratic: x^2 – 8x + 16 = 0. This factors to (x – 4)^2 = 0. Therefore, x = 4. Now, substitute x = 4 into the expression x^2 + 32/x^2: 4^2 + 32/4^2 = 16 + 32/16 = 16 + 2 = 18.
Correct Option: B
Q. 4 Given that the sum of three variables (x, y, and z) is 2 and the sum of their pairwise products is -11, what is the value of the expression x³ + y³ + z³ – 3xyz?
Check Solution
Ans: B
Explanation: We are given x + y + z = 2 and xy + yz + zx = -11. We need to find the value of x³ + y³ + z³ – 3xyz. We can use the identity:
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
We also know that (x + y + z)² = x² + y² + z² + 2(xy + yz + zx). Thus,
x² + y² + z² = (x + y + z)² – 2(xy + yz + zx)
x² + y² + z² = (2)² – 2(-11) = 4 + 22 = 26
Now substitute into the first equation:
x³ + y³ + z³ – 3xyz = (x + y + z)[(x² + y² + z²) – (xy + yz + zx)]
x³ + y³ + z³ – 3xyz = (2)[26 – (-11)]
x³ + y³ + z³ – 3xyz = 2(26 + 11)
x³ + y³ + z³ – 3xyz = 2(37) = 74
Correct Option: B
Q. 5 Given the equation $a^2 + b^2 + 49c^2 + 18 = 2(b – 28c – a)$, find the value of $(a – b – 7c)$.
Check Solution
Ans: C
Explanation: First, rearrange the given equation:
$a^2 + b^2 + 49c^2 + 18 = 2b – 56c – 2a$
$a^2 + 2a + b^2 – 2b + 49c^2 + 56c + 18 = 0$
Complete the square for each variable:
$(a^2 + 2a + 1) + (b^2 – 2b + 1) + (49c^2 + 56c + 16) + 18 – 1 – 1 – 16 = 0$
$(a + 1)^2 + (b – 1)^2 + (7c + 4)^2 = 0$
Since the sum of squares is equal to zero, each term must be zero. Therefore:
$a + 1 = 0 \implies a = -1$
$b – 1 = 0 \implies b = 1$
$7c + 4 = 0 \implies c = -4/7$
Now, substitute these values into the expression $a – b – 7c$:
$a – b – 7c = -1 – 1 – 7(-4/7)$
$= -2 + 4$
$= 2$
Correct Option: C
Q. 6 Given the equation $27x^3 – 64y^3 = (Ax + By)(Cx^2 – Dy^2 + 12xy)$, find the value of $4A + B + 3C + 2D$.
Check Solution
Ans: B
Explanation: The given equation is a factorization of the difference of cubes. We can rewrite the left side as:
$27x^3 – 64y^3 = (3x)^3 – (4y)^3$
Using the difference of cubes factorization formula: $a^3 – b^3 = (a – b)(a^2 + ab + b^2)$, we can factorize the left side as follows:
$ (3x)^3 – (4y)^3 = (3x – 4y)((3x)^2 + (3x)(4y) + (4y)^2) $
$ (3x – 4y)(9x^2 + 12xy + 16y^2) $
Now, comparing this to the right side of the given equation:
$ (Ax + By)(Cx^2 – Dy^2 + 12xy) = (3x – 4y)(9x^2 + 12xy + 16y^2) $
By comparing the terms, we can deduce:
A = 3, B = -4, C = 9, and D = -16
Now, we can find the value of $4A + B + 3C + 2D$:
$4A + B + 3C + 2D = 4(3) + (-4) + 3(9) + 2(-16)$
$ = 12 – 4 + 27 – 32$
$ = 3$
Correct Option: B
Q. 7 Given the equation $x^2 + 9y^2 + 4z^2 = 12(x – 2y + 2z) – 88$, what is the value of $(x – 3y + z)$?
Check Solution
Ans: A
Explanation: First, rearrange the given equation by moving all terms to the left side:
$x^2 – 12x + 9y^2 + 24y + 4z^2 – 24z + 88 = 0$
Complete the square for x, y, and z terms.
$x^2 – 12x + 36 + 9y^2 + 24y + 16 + 4z^2 – 24z + 36 + 88 – 36 – 16 – 36 = 0$
$(x – 6)^2 + 9(y^2 + \frac{24}{9}y + \frac{16}{9}) + 4(z^2 – 6z + 9) = 0$
$(x – 6)^2 + (3y + 4/3 * 3/1)^2 + 4(z – 3)^2 – 88 + 36 + 16 + 36=0 $
$(x^2 -12x +36) + (9y^2 + 24y + 16) + (4z^2 – 24z + 36) = 0$
$(x – 6)^2 + (3y + 4)^2 + 4(z-3)^2 = 0$\
$(x-6)^2 + (3(y+4/3))^2 + (2(z-3))^2 = 0$
$(x – 6)^2 + (3y + 4)^2 + (2z – 6)^2 = 0$
This is not zero
$(x^2 – 12x + 36) + (9y^2 + 24y + 16) + (4z^2 – 24z + 36) + 88 – 36 – 16 – 36 = 0$
$(x-6)^2 + (3y + 4)^2 + (2z – 6)^2 = 0$
$x-6=0$, $3y + 4 =0$ and $2z-6 =0$
So, $x=6$, $y = -4/3$, $z = 3$
Then we have $(x – 3y + z) = 6 – 3(-4/3) + 3 = 6 + 4 + 3 = 13$
Correct Option: A
Q. 8 Given the equation y = 2x + 1, find the value of the expression 8x³ – y³ + 6xy.
Check Solution
Ans: B
Explanation: We are given y = 2x + 1. We want to find the value of 8x³ – y³ + 6xy.
Substitute y = 2x + 1 into the expression:
8x³ – (2x + 1)³ + 6x(2x + 1)
Expand (2x + 1)³ = (2x + 1)(2x + 1)(2x + 1) = (4x² + 4x + 1)(2x + 1) = 8x³ + 4x² + 8x² + 4x + 2x + 1 = 8x³ + 12x² + 6x + 1
So the expression becomes:
8x³ – (8x³ + 12x² + 6x + 1) + 12x² + 6x
= 8x³ – 8x³ – 12x² – 6x – 1 + 12x² + 6x
= (8x³ – 8x³) + (-12x² + 12x²) + (-6x + 6x) – 1
= 0 + 0 + 0 – 1
= -1
Correct Option: B
Q. 9 Given three numbers, a, b, and c, that satisfy the following equations: their sum is 1, the sum of their pairwise products is -22, and their product is -40. Calculate the value of a³ + b³ + c³.
Check Solution
Ans: A
Explanation: We are given:
a + b + c = 1
ab + bc + ca = -22
abc = -40
We want to find a³ + b³ + c³.
We can use the identity:
a³ + b³ + c³ – 3abc = (a + b + c)(a² + b² + c² – ab – bc – ca)
We also know that:
(a + b + c)² = a² + b² + c² + 2(ab + bc + ca)
1² = a² + b² + c² + 2(-22)
1 = a² + b² + c² – 44
a² + b² + c² = 45
Now, substitute the known values into the identity:
a³ + b³ + c³ – 3(-40) = (1)(45 – (-22))
a³ + b³ + c³ + 120 = 1(45 + 22)
a³ + b³ + c³ + 120 = 67
a³ + b³ + c³ = 67 – 120
a³ + b³ + c³ = -53
Correct Option: A
Q. 10 Given two positive numbers, *a* and *b*, that satisfy the equations 4*a* – 3*b* = 1 and *a* *b* = 1/2, calculate the value of 64*a*³ + 27*b*³.
Check Solution
Ans: C
Explanation: We are given two equations: 4a – 3b = 1 and ab = 1/2. We want to find the value of 64a³ + 27b³. Notice that 64a³ = (4a)³ and 27b³ = (3b)³. We can rewrite the expression as (4a)³ + (3b)³. We can use the sum of cubes factorization: x³ + y³ = (x + y)(x² – xy + y²). Let x = 4a and y = 3b. Then, (4a)³ + (3b)³ = (4a + 3b)((4a)² – (4a)(3b) + (3b)²). We know 4a – 3b = 1 and ab = 1/2.
First, we need to find 4a + 3b. Square the equation 4a – 3b = 1: (4a – 3b)² = 1. This gives us 16a² – 24ab + 9b² = 1. We know ab = 1/2, so 24ab = 24*(1/2) = 12. Thus, 16a² – 12 + 9b² = 1. This implies 16a² + 9b² = 13.
Now consider (4a + 3b)² = (4a)² + 2(4a)(3b) + (3b)² = 16a² + 24ab + 9b² = 16a² + 9b² + 24ab = 13 + 12 = 25. Then, 4a + 3b = sqrt(25) = 5 (since a and b are positive).
Now, (4a)³ + (3b)³ = (4a + 3b)((4a)² – (4a)(3b) + (3b)²) = (4a + 3b)(16a² – 12ab + 9b²) = (4a + 3b)(16a² + 9b² – 12ab). We have 4a + 3b = 5, 16a² + 9b² = 13 and ab = 1/2 so 12ab = 6. Substituting, 64a³ + 27b³ = (5)(13 – 12(1/2)) = 5(13 – 6) = 5 * 7 = 35. Therefore the original expression (4a)³+(3b)³ = (4a+3b)((4a)²-4a(3b)+(3b)²) = (4a+3b)(16a²-12ab+9b²). We have 4a+3b = 5. (4a-3b)=1. Square (4a+3b)² = 16a²+24ab+9b². (4a-3b)²=16a²-24ab+9b². 16a²-12+9b²=1. 16a²+9b²=13. 64a³+27b³ = (4a+3b)(16a²-12ab+9b²) = (4a+3b)(16a²+9b²-12ab) = (5)(13-12(1/2)) = (5)(13-6) = 35.
Correct Option: C
Q. 11 If $y – \frac{1}{y} = 4$, then the value of $y^3 – \frac{1}{y^3}$ is:
Check Solution
Ans: D
Explanation: We are given $y – \frac{1}{y} = 4$. We want to find the value of $y^3 – \frac{1}{y^3}$.
Recall the identity: $a^3 – b^3 = (a – b)(a^2 + ab + b^2)$.
Let $a = y$ and $b = \frac{1}{y}$. Then
$y^3 – \frac{1}{y^3} = (y – \frac{1}{y})(y^2 + y(\frac{1}{y}) + \frac{1}{y^2})$
$y^3 – \frac{1}{y^3} = (y – \frac{1}{y})(y^2 + 1 + \frac{1}{y^2})$
We know $y – \frac{1}{y} = 4$. Also, $ (y – \frac{1}{y})^2 = y^2 – 2 + \frac{1}{y^2}$.
So, $4^2 = y^2 – 2 + \frac{1}{y^2}$, which implies $16 = y^2 – 2 + \frac{1}{y^2}$. Therefore, $y^2 + \frac{1}{y^2} = 18$.
Now substitute this back into our expression for $y^3 – \frac{1}{y^3}$:
$y^3 – \frac{1}{y^3} = (4)(y^2 + 1 + \frac{1}{y^2})$
$y^3 – \frac{1}{y^3} = (4)(18 + 1)$
$y^3 – \frac{1}{y^3} = (4)(19)$
$y^3 – \frac{1}{y^3} = 76$
Q. 12 If $x^3 – \frac{1}{x^3} = 14$, then the value of $x – \frac{1}{x}$ is:
Check Solution
Ans: C
Explanation: Let $y = x – \frac{1}{x}$. We want to find the value of $y$.
We know that $(x – \frac{1}{x})^3 = x^3 – 3x^2(\frac{1}{x}) + 3x(\frac{1}{x^2}) – \frac{1}{x^3}$
$(x – \frac{1}{x})^3 = x^3 – 3x + \frac{3}{x} – \frac{1}{x^3}$
$(x – \frac{1}{x})^3 = x^3 – \frac{1}{x^3} – 3(x – \frac{1}{x})$
So, $y^3 = x^3 – \frac{1}{x^3} – 3y$
We are given $x^3 – \frac{1}{x^3} = 14$.
Substituting this into the equation, we get $y^3 = 14 – 3y$
$y^3 + 3y – 14 = 0$
By observation, if $y=2$, then $2^3 + 3(2) – 14 = 8 + 6 – 14 = 0$
Thus $y=2$ is a solution.
So, $x – \frac{1}{x} = 2$
Q. 13 If $y+\frac{1}{y}=4$, then the value of $y^3+\frac{1}{y^3}$ is:
Check Solution
Ans: B
Explanation: We are given `y + 1/y = 4` and we need to find `y^3 + 1/y^3`. We can use the identity: `(a + b)^3 = a^3 + b^3 + 3ab(a + b)`. Let `a = y` and `b = 1/y`. Then, `(y + 1/y)^3 = y^3 + 1/y^3 + 3 * y * (1/y) * (y + 1/y)`. Substituting the given value, `4^3 = y^3 + 1/y^3 + 3 * 1 * 4`. So, `64 = y^3 + 1/y^3 + 12`. Therefore, `y^3 + 1/y^3 = 64 – 12 = 52`.
Next Chapter: Analogy
Crack SSC CGL – with LearnTheta’s AI Platform!
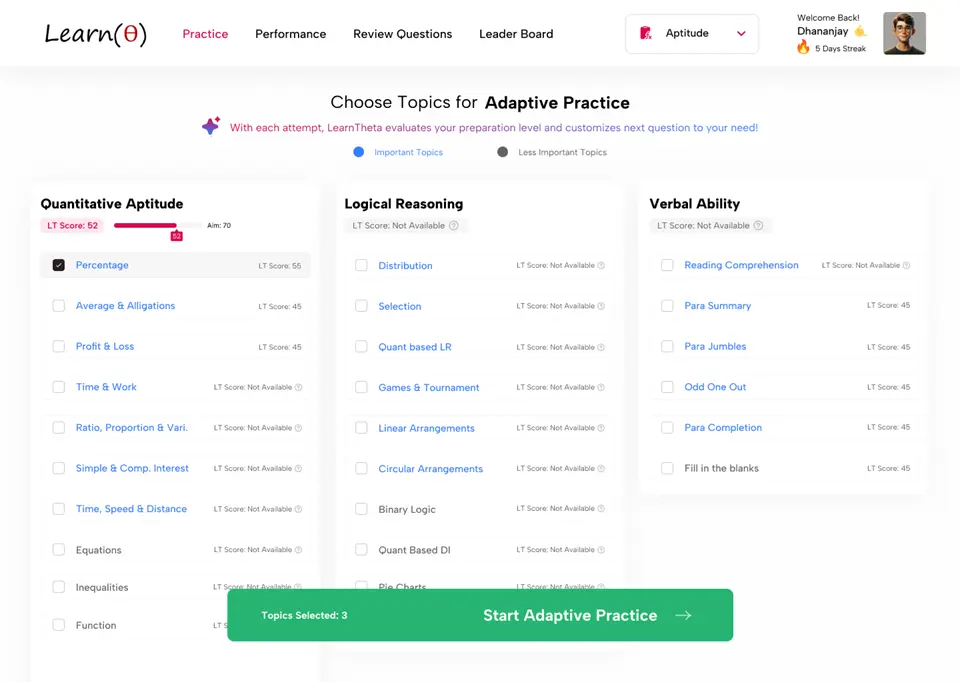
✅ All Topics at One Place
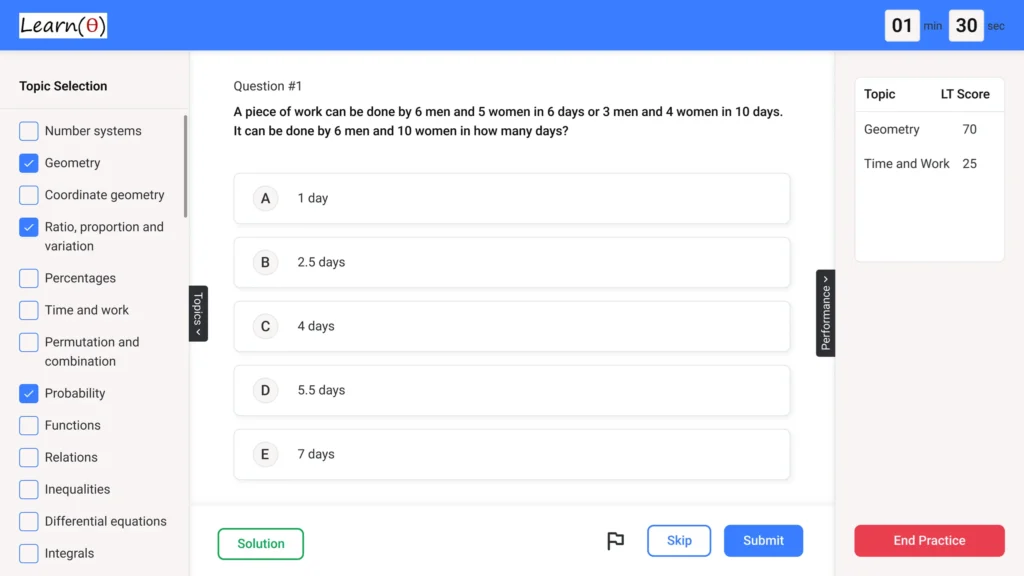
🤖 Adaptive Question Practice
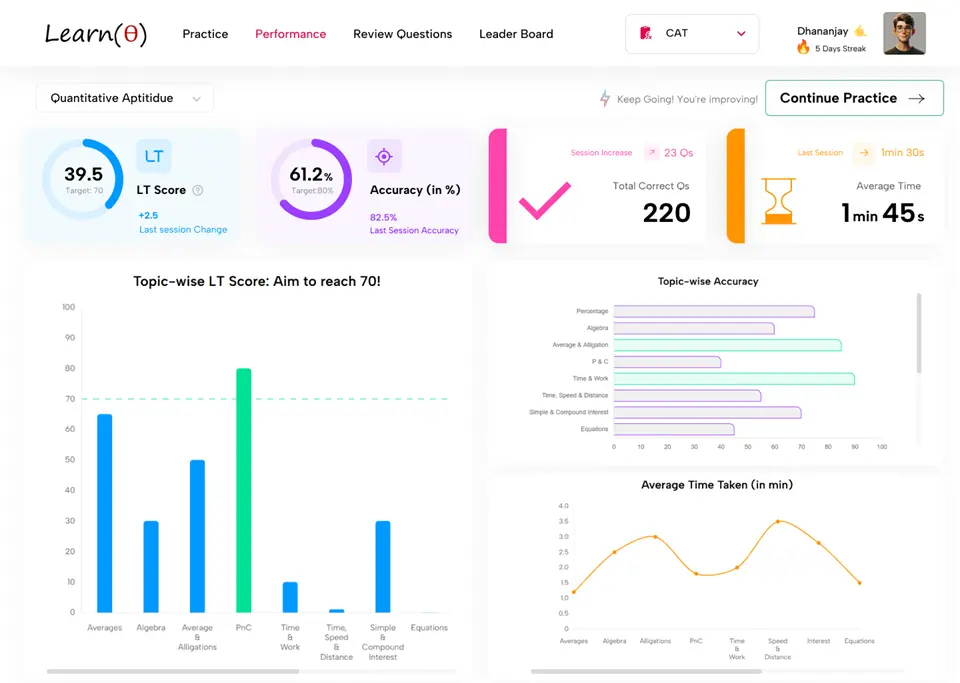
📊 Progress and Insights